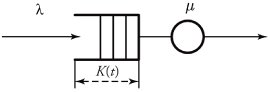
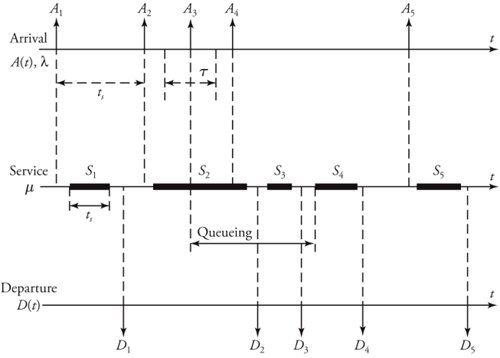
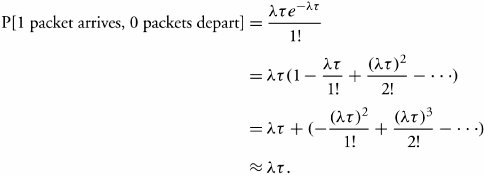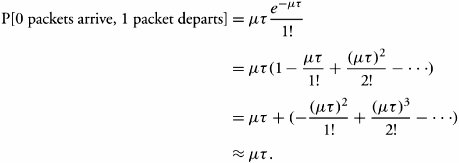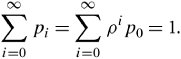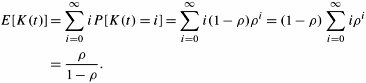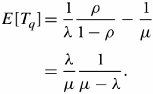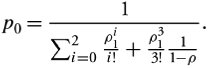Section 11.4. Markovian FIFO Queueing Systems
| Example. | Use Little's formula to find the mean number of packets in the queue. |
| Solution. | Little's formula can be applied in most stochastic systems, such as a queue defined solely as a system. If E [ K q (t) ] is the mean number of packets in the queue: Interestingly, the mean number of packets is a function only of utilization. In other words, the value of utilization in any single-queue system determines the average number of packets in the system. |
11.4.2. Systems with Limited Queueing Space: M/M/1/b
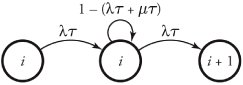
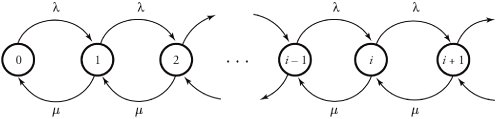
In a queue with exponential interarrival times and exponential service times, a single server and a maximum of b packets can be held in the system. Once such a system exceeds its capacity, arriving packet numbered b + 1 is turned away from the system, since there is no room for it. Figure 11.8 shows the state-transition diagram for the M/M/ 1 /b system. This diagram is a Markov chain and is very similar to the one illustrated in Figure 11.7, but the chain for the M/M/ 1 /b system stops at the maximum capacity of b . Thus, the global balance equations use the same results presented in Equation(11.18), where the sum of all probabilities is always 1 and thus
Equation 11.24
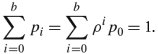
Figure 11.8. State-transition diagram for M/M/ 1 /b system
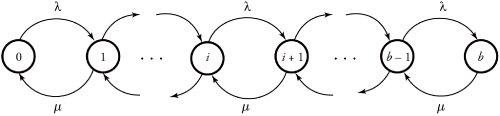
A stable situation exists when the arrival rate is less than the service rate, or = »/ µ < 1, in which case K(t) does not increase in value without bound and therefore ![]() . This fact simplifies Equation (11.17) for deriving the number of packets in the system, which is a continuous-time Markov chain taking on values from the set {0, 1, ..., b }:
. This fact simplifies Equation (11.17) for deriving the number of packets in the system, which is a continuous-time Markov chain taking on values from the set {0, 1, ..., b }:
Equation 11.25
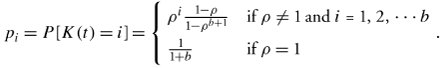
Note that the number of packets in the system is derived in two parts , depending on whether the utilization is maximized ( = 1) or not.
Mean Number of Packets
The mean number of packets in the system, E [ K(t) ], can be expressed by Formula C.20 in Appendix C:
Equation 11.26
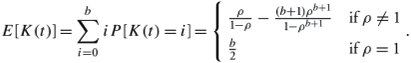
Clearly, results of the mean number of packets in the M/M/ 1 and M/M/ 1 /b systems are fundamentally different, owing to the difference in capacities available in these two systems.
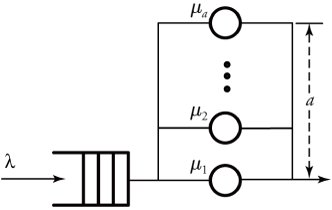
11.4.3. M/M/a Queueing Systems
Some stochastic systems are modeled by M/M/a , where a servers instead of one can be used to enhance system performance, as shown in Figure 11.9. The service rate in each server may be different from or equal to that in the others, as rates µ 1 through µ a are indicated as service rates of the corresponding servers. The advantage of this discipline over systems with one server is its parallel-serving feature. A packet can be partitioned into i < a different tasks and served in parallel in i different servers concurrently.
Figure 11.9. Queueing model of M/M/a systems
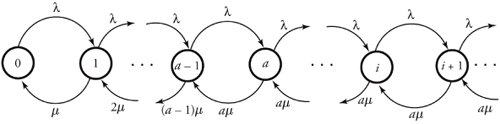
The resulting system can be modeled by a continuous-time Markov chain, as shown in Figure 11.10. The maximum number of servers is denoted by a . As long as the number of packets in the queue is less than a , the service rate is proportionally changing ( i µ ) with the number of waiting packets while the arrival rate remains constant. However, when the number of packets in the queue reaches a , the arrival rate stays constant at its maximum of a µ .
Figure 11.10. State-transition diagram for M/M/a systems
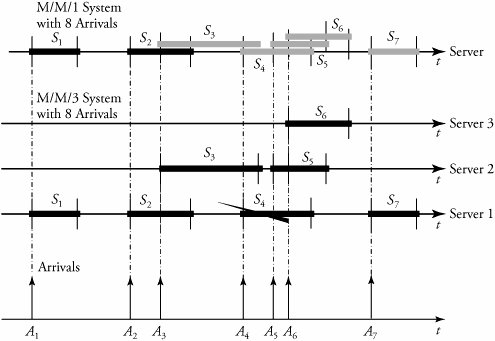
| Example. | Figure 11.11 shows a statistical comparison between M/M/ 1 and M/M/ 3 systems, each with seven packets. In the M/M/ 1 system, the third packet, S 3 , starts to accumulate in the queue. The queueing trend continues, as shown by gray, if the service rate stays low. On the contrary, in the M/M/ 3 system, packets are distributed over the three servers on arrival, and queueing has not happened . Figure 11.11. Comparison of M/M/ 1 and M/M/ 3 systems, each with seven packets |
Balance Equations for i  a
a
The steady-state probabilities for the M/M/a system can be obtained by using the birth-and-death process. Balance equations for i servers being busy when i 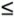 a begin with p i :
a begin with p i :
Equation 11.27
![]()
Recall that ![]() is the utilization and that p i = ( 1 2 ... i - 1 i )p . Thus, p i can be rewritten as
is the utilization and that p i = ( 1 2 ... i - 1 i )p . Thus, p i can be rewritten as
Equation 11.28
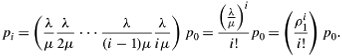
It is easy to realize the probability that all servers are in use. Substitute i = a in Equation (11.28):
Equation 11.29
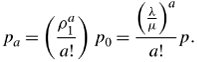
Balance Equations for i  a
a
To determine the balance equations for i 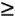 a , we again use the birth-and-death process. The second part of the transition diagram, starting from state a , is formulated over states i = a , a + 1, a + 2, .... As a result, the birth-and-death process formula is set up by
a , we again use the birth-and-death process. The second part of the transition diagram, starting from state a , is formulated over states i = a , a + 1, a + 2, .... As a result, the birth-and-death process formula is set up by
Equation 11.30
![]()
where = ![]() . In this equation, p a can be substituted by the value obtained last from the case of i
. In this equation, p a can be substituted by the value obtained last from the case of i 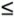 a , presented in Equation (11.29). Therefore, by replacing p a with
a , presented in Equation (11.29). Therefore, by replacing p a with ![]() , we obtain
, we obtain
Equation 11.31
![]()
Equations (11.28) and (11.31) together cover all the cases in the state diagram. Since the sum of all probabilities is always 1, ![]()
Equation 11.32
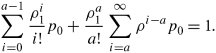
To have a stable system, we want < 1, which causes ![]() to converge to
to converge to ![]() . With this simplification, we can compute the probability of the first state from Equation 11.32:
. With this simplification, we can compute the probability of the first state from Equation 11.32:
Equation 11.33
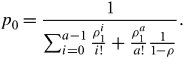
Similar to previous cases, knowing p is essential, as we can derive p i from Equation (11.31).
In an M/M/a system, we can use the Erlang-C formula to compute the blocking probability. This formula calculates the probability that an arriving packet finds all servers busy. This probability is the same as the probability that the waiting time for the packet in the queue is greater than zero, or the probability that the number of packets in the queueing system is greater than or equal to a , P [ K(t) 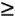 a ]:
a ]:
Equation 11.34
![]()
As with the M/M/ 1 queueing system, we can now estimate all the parameters for the M/M/a discipline. The mean number of packets in the queue is
Equation 11.35
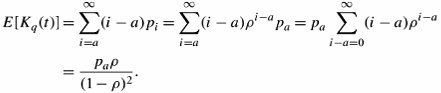
Accordingly, the mean packet delay in the queue is
Equation 11.36
![]()
Obviously, the total mean packet delay in a system is
Equation 11.37
![]()
The mean number of packets in the system is obtained again from Little's formula:
Equation 11.38
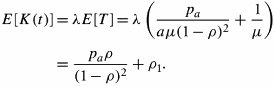
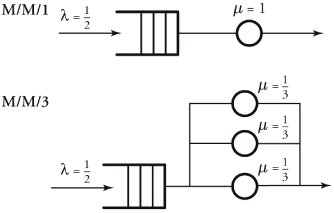
| Example. | A communication node receives packets at » = 1/2 packet per nanosecond, and the switching server processes packets at the rate of one packet per nanosecond. Calculate the queueing delay and the total node's delay, and then compare the results for using queueing disciplines M/M/ 1 and M/M/ 3 with equal service powers as shown in Figure 11.12. Figure 11.12. Two queueing disciplines with equal service powers |
| Solution. | With an M/M/ 1 discipline, = »/ µ = 0.5. So the mean queueing delay is Equation 11.39 and the total node's delay is Equation 11.40 For the M/M/ 3 discipline, a = 3 servers are used; thus, 1 = »/ µ = 1.5, and = »/a µ = 0.5. Thus: Equation 11.41 Since Equation 11.42 and the total mean node's delay is Equation 11.43 |
This useful example expresses an important conclusion: Increasing the number of servers lowers the queueing delay but increases the total system delay. In summary, compared with the M/M/a system ( a> 1), the M/M/ 1 system has a smaller total delay but a larger queueing delay. However, note that the preceding statement should be made with an important condition; that is, the total service rates of a servers in the M/M/a model must be equal to the service rate of the M/M/ 1 model.
11.4.4. Models for Delay-Sensitive Traffic: M/M/a/a
Some network nodes can be built with no buffering elements. One application of such systems is for cases in which delay-sensitive traffic , such as voice, needs a queueless service. These types of nodes can be shown by queueless models. One example of such models is the M/M/a/a queueing system, which has a servers but no queueing line. If all servers are busy, an arriving packet is turned away, resulting in the transition-rate diagram shown in Figure 11.13. This transition rate partially resembles that for an M/M/a system. Thus, we use the previously obtained equation for the probability that the system is in state i ˆˆ{0, ..., a }:
Equation 11.44
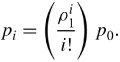
Figure 11.13. State-transition diagram for M/M/a/a systems
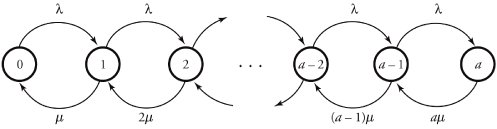
Combining Equation (11.44) and the fact that ![]() gives us
gives us
Equation 11.45
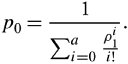
Erlang-B Blocking Probability
In an M/M/a/a system, we can compute the blocking probability, this time using the Erlang-B formula . This formula calculates the probability that an arriving packet finds all servers busy but no waiting line for packets. The probability that all servers of the system are busy is referred to as the Erlang-B formula , using Equation (11.44) with i = a :
Equation 11.46
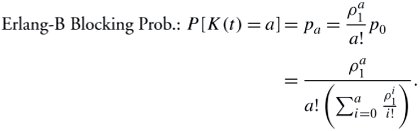
When all servers are busy, an incoming packet is turned away. Let » , » p , and » b = p a » represent the arrival rate, the packet-passing rate, and the blocking rate, respectively. Therefore, » = » p + » b . The packet-passing rate can then be rewritten as » p = »( 1 - p a ) . In such systems, it would be interesting to find the average number of packets in the system, since no queueing line exists. From Little's formula:
Equation 11.47
![]()
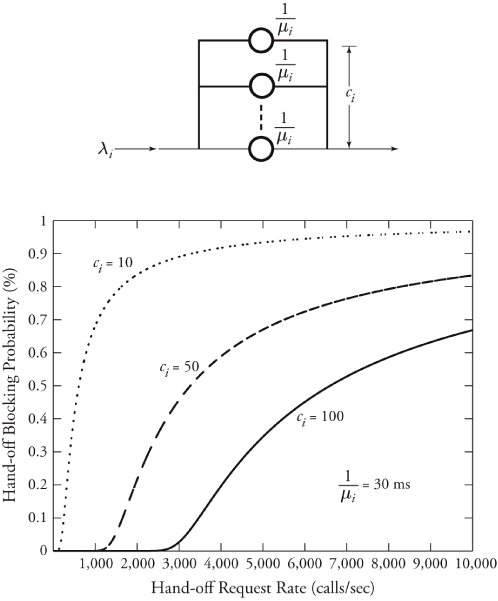
| Example. | When a mobile user in a wireless data network moves to a new region, a handoff process between the two regions needs to take place. If all the new region's channels are used, the handoff call is terminated or blocked. For real-time communications, this scenario is modeled by an M/M/a/a system, where a = c i is the number of handoff servers of traffic type i . Assume that c i =10, 50, and 100; mean service time 1 / µ i = 30 msec; and handoff request rate » i = 0 ... 10, 000. Sketch a set of plots showing the performance of the handoff process. |
| Solution. | The calculation effort is left to readers. Instead, the results of the computations in Figure 11.14 are given. The plots in this figure depict the results of an M/M/a/a model for the wireless handoff. Equation (11.46) can be used to compute the handoff blocking probability. Figure 11.14. A wireless data network model as an M/M/a/a system with c i channel servers |
11.4.5. M/M/  Queueing Systems
Queueing Systems
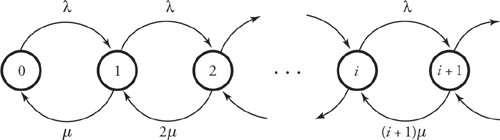
In many high-speed network nodes, higher cost can be tolerated in exchange for better communication quality. One method of improving the quality of handling packets is to consider a large number of servers at a node. If we let a approach a real large number approximated to infinity, an M/M/a/a system becomes an M/M/  system. As a result, the transition-rate diagram can continue to
system. As a result, the transition-rate diagram can continue to  , as shown in Figure 11.15. To find steady-state probabilities, p i , for this queueing system, we use Equation (11.46) of the M/M/a/a system and let a be a number i varying up to
, as shown in Figure 11.15. To find steady-state probabilities, p i , for this queueing system, we use Equation (11.46) of the M/M/a/a system and let a be a number i varying up to  :
:
Equation 11.48
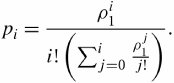
Figure 11.15. State-transition diagram for M/M/  system
system
In the denominator of this equation, ![]() tends to converge to e 1 when i approaches infinity:
tends to converge to e 1 when i approaches infinity:
Equation 11.49
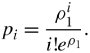
EAN: 2147483647
Pages: 211