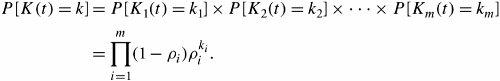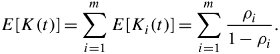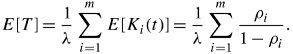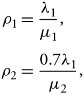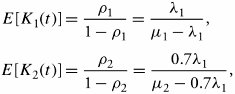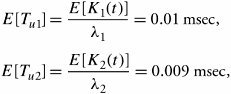Section 11.6. Networks of Queues

11.6. Networks of Queues

Networks of queueing nodes can be modeled and their behavior, including feedback, studied. Two important and fundamental theorems are Burke's theorem and Jackson's theorem . Burke's theorem presents solutions to a network of several queues. Jackson's theorem is relevant when a packet visits a particular queue more than once.

11.6.1. Burke's Theorem

When a number of queueing nodes are connected, they all may be either in series or in parallel. In such circumstances, the entire system requires a careful and justified procedure for modeling. Burke's theorem presents solutions to a network of m queues: m queueing nodes in series and m queueing nodes in parallel.

Burke's Theorem on Cascaded Nodes

One common case is cascaded queueing nodes, as shown in Figure 11.18. In this network, the departure of a packet from a queueing node i is the arrival for node i + 1. The utilization for any node i is _i = »/¼ _i , where » and ¼ _i are the arrival rate and service rate of that node, respectively.

Figure 11.18. Burke's theorem applied on m cascaded queues

The packet-movement activity of this network is modeled by an m -dimensional Markov chain. For simplicity, consider a two-node network of Nodes 1 and 2. Figure 11.19 shows a two-dimensional Markov chain for this simplified network. The chain starts at state 00. When the first packet arrives at rate » , the chain goes to state 01. At this point, the chain can return to state 10 if it gets serviced at rate ¼ ₁ , since the packet is now in node 2. If the packet is sent out of the second node at service rate µ ₂ , the chain returns to state 00, showing the empty status of the system. The Markov chain can be interpreted similarly for a larger number of packets.

Figure 11.19. Two-dimensional Markov chain of the first two cascaded queues in Figure 11.18

In our system with m nodes, assume an M/M/ 1 discipline for every node; the probability that k packets are in the system, P [ K(t) = k ], is:

Equation 11.62

The expected number of packets in each node, E [ K _i (t) ], can easily be estimated by using the M/M/ 1 property of each node:

Equation 11.63

Therefore, the expected number of packets in the entire system is derived by

Equation 11.64

We can now use Little's formula to estimate the total queueing delay that a packet should expect in the entire system:

Equation 11.65

This last important result can help estimate the speed of a particular system modeled by a series of queueing nodes.

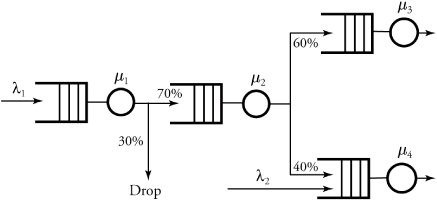
Example.

Figure 11.20 shows four queueing nodes. There are two external sources at rates: » 1 = 2 million packets per second and » 2 = 0.5 million packets per second. Assume that all service rates are identical and equal to ¼ 1 = ¼ 2 = ¼ 3 = ¼ 4 = 2.2 million packets per second. Find the average delay on a packet passing through nodes 1, 2, and 4. Figure 11.20. A Four-queueing-node system solved using Burke's theorem

Solution.

The figure shows the utilizations as and The expected numbers of packets in nodes 1, 2 and 4 are, respectively: and The expected overall delay, then, is

Burke's Theorem on Parallel Nodes

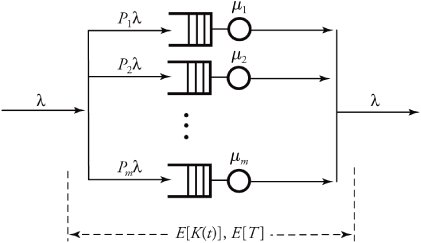
We can now easily apply Burke's theorem in cases of in-parallel queueing nodes, as shown in Figure 11.21. Suppose that the incoming traffic with rate » is distributed over m parallel queueing nodes with probabilities P ₁ through P _m , respectively. Also assume that the queuing nodes' service rates are ¼ ₁ through ¼ _m , respectively. In this system, the utilization for any node i is expressed by

Equation 11.66

Figure 11.21. Application of Burke's theorem on parallel nodes

Assuming that each node is represented by an M/M/ 1 queueing model, we calculate the expected number of packets in the queue of a given node i by

Equation 11.67

But the main difference between a cascaded queueing system and a parallel queueing system starts here, at the analysis on average delay. In the parallel system, the overall average number of packets, , is an irrelevant metric. The new argument is that a packet has a random chance of P _i to choose only one of the m nodes (node i ) and thus is not exposed to all m nodes. Consequently, we must calculate the average number of queued packets that a new arriving packet faces in a branch i . This average turns out to have a perfect stochastic pattern and is obtained by E [ K(t) ]:

Equation 11.68

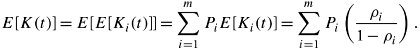
Using Little's formula, we can first estimate the delay incurred in branch i :

Equation 11.69

Now, the total queueing delay that a packet should expect in the entire system, E [ T ], is the average delay over all m parallel branches. This delay is, in fact, a stochastic mean delay of all parallel branches, as follows :

Equation 11.70

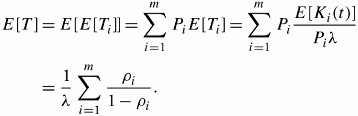
Obviously, E [ T ] can help us estimate the speed of a particular m parallel-node system. An important note here is that Equations (11.64) and (11.68) may look the same. But the fact is that since the utilization in the case of cascaded nodes, _i = » _i /¼ _i , and the one for parallel nodes, _i = P _i » _i /¼ _i , are different, the results of E [ K(t) ] in these cases too are different. We can argue identically on E [ T ] for the two cases. Although Equations (11.65) and (11.70) are similar, we should expect the overall delay in the parallel-node case to be far less than the one for in-series case, owing to the same reason.

11.6.2. Jackson's Theorem

One of the most frequently applied theorems in analyzing a network of queues is known as Jackson's theorem , which has several segments. Here, we emphasize the most applicable phase, known as open networks of queues. The essence of Jackson's theorem is applied to situations in which a packet visits a particular queue more than once. In such conditions, the network typically contains loops , or feedback .

Modeling Feedback in Networks

Figure 11.22 shows a basic cascaded queueing network, including a simple M/M/ 1 queueing element with a server in which simple feedback is implemented. Packets arrive at the left at rate ± , passing through a queue and server with service rate ¼ and are partially fed back to the system at rate ± ₁ . Thus, this queueing architecture allows packets to visit the queue more than once by circulating them back to the system. This system is a model of many practical networking systems. One good example is switching systems that multicast packets step by step, using a recycling technique discussed in later chapters. In Figure 11.22, if the probability that a packet is fed back to the input is p , it is obvious that the total arrival rate to the queue, or » , is

Equation 11.71

Figure 11.22. A feedback system and its simplified equivalent

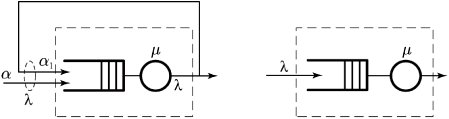
Equation (11.71) demonstrates that the equivalent of the system surrounded by the dashed line can be configured as shown in Figure 11.22. Since ± ₁ = p» , we can combine this equation and Equation 11.71 and derive a relationship between » and ± as

Equation 11.72

The utilization of the simplified system denoted by is, clearly:

Equation 11.73

By having the utilization of the system, we can derive the probability that k packets are in the system, P [ K(t) = k ], knowing that the system follows the M/M/ 1 rule:

Equation 11.74

The expected number of packets in the system, E [ K(t) ], can be derived by using the M/M/ 1 property:

Equation 11.75

Using Little's formula, we can now estimate the total queueing and service delay that a packet should expect. Let E [ T _u ] be the expected delay for the equivalent unit shown in Figure 11.22 with lump sum arrival rate » . Let E [ T _f ] be the expected delay for the system with arrival rate ± :

Equation 11.76

and

Equation 11.77

Note that we should always see the inequity E [ T _u ] <E [ T _f ] as expected.

Open Networks

Figure 11.23 shows a generic model of Jackson's theorem when the system is open. In this figure, unit i of an m -unit system is modeled with an arrival rate sum of » _i and a service rate ¼ _i . Unit i may receive an independent external traffic of ± _i . The unit can receive feedback and feed-forward traffic from i - 1 other units. At the output of this unit, the traffic may proceed forward with probability P _{ii +1} or may leave the system with probability 1 - P _{ii +1} . The total arrival rate, » _i , is then

Equation 11.78

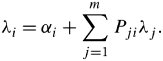
Figure 11.23. Generalization of a node model for Jackson's theorem

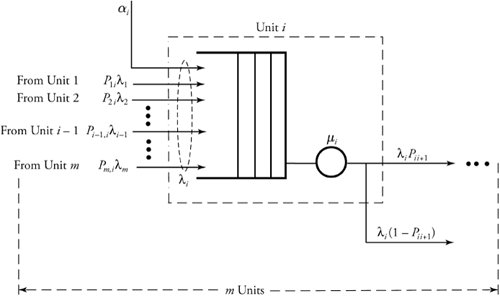
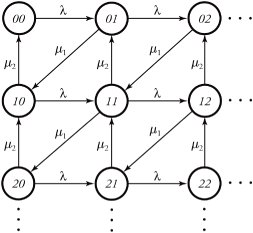
The instantaneous total number of packets in all m nodes, K(t) , is a vector consist of the number of packets in every individual node and is expressed by

Equation 11.79

The probability that k packets are in the system is the joint probabilities of numbers of packets in m units:

Equation 11.80

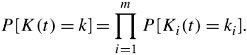
The expected number of packets in all units is obtained by

Equation 11.81

Finally, the most significant factor used in evaluating a system of queueing nodes, total delay at stage i , is calculated by applying Little's formula:

Equation 11.82

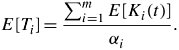
We assume that ± _i is the only input to the entire system. In practice, there may be other inputs to the system, in which case the total delay can be obtained by using superposition . Equations (11.80) through (11.82) are the essence of Jackson's theorem on open queueing networks.

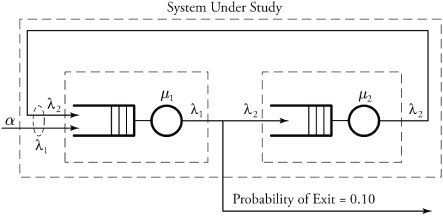
Example.	Figure 11.24 shows a cascade of two M/M/ 1 nodes in which packets arrive at rate ± = 10, 000 packets per second. Service rates of both nodes are ¼ 1 = ¼ 2 = 200, 000 packets per second. At the output of node 1, packets exit with probability of p = 0.10; otherwise , they are driven into node 2 and then fed back to node 1. Find the estimated delay incurred on a packet, including the delay from circulations. Figure 11.24. Two communication nodes with feedback
Solution.	We first calculate the arrival rates to two nodes, » 1 and » 2 : » 1 =» 2 +± and » 2 =(1- p )» 1 . By applying the values of ± = 10, 000 and p = 0.10, this set of equations results in » 1 = 100, 000 and » 2 = 90, 000. The utilization for each system can now be derived as 1 = » 1 /¼ 1 = 0.5 and 2 = » 2 /¼ 2 = 0.45. According to M/M/ 1 discipline results obtained in the previous chapter, the average number of packets in each system is and The delay is and