Chapter 30: Using Solver for Capital Budgeting

Overview

• How can a company use Solver to determine which projects it should undertake?

Each year, a company like Eli Lilly needs to determine which drugs to develop; a company like Microsoft, which software programs to develop; a company like Proctor & Gamble, which new consumer products to develop. The Solver feature in Microsoft Office Excel 2007 can help a company make these decisions.

• How can a company use Solver to determine which projects it should undertake?

  Most corporations want to undertake projects that contribute the greatest net present value (NPV), subject to limited resources (usually capital and labor). Let’s say that a software development company is trying to determine which of 20 software projects it should undertake. The NPV (in millions of dollars) contributed by each project as well as the capital (in millions of dollars) and the number of programmers needed during each of the next three years is given on the Basic Model worksheet in the file Capbudget.xlsx, which is shown in Figure 30-1 on the next page. For example, Project 2 yields $908 million. It requires $151 million during Year 1, $269 million during Year 2, and $248 million during Year 3. Project 2 requires 139 programmers during Year 1, 86 programmers during Year 2, and 83 programmers during Year 3. Cells E4:G4 show the capital (in millions of dollars) available during each of the three years, and cells H4:J4 indicate how many programmers are available. For example, during Year 1 up to $2.5 billion in capital and 900 programmers are available.

  The company must decide whether it should undertake each project. Let’s assume that we can’t undertake a fraction of a software project; if we allocate 0.5 of the needed resources, for example, we would have a nonworking program that would bring us $0 revenue!

  The trick in modeling situations in which you either do or don’t do something is to use binary changing cells. A binary changing cell always equals 0 or 1. When a binary changing cell that corresponds to a project equals 1, we do the project. If a binary changing cell that corresponds to a project equals 0, we don’t do the project. You set up Solver to use a range of binary changing cells by adding a constraint-select the changing cells you want to use and then choose Bin from the list in the Add Constraint dialog box.

  
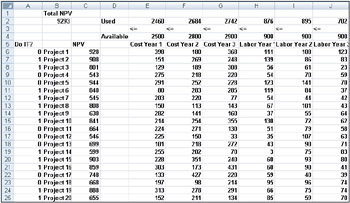
  Figure 30-1: Data we will use with Solver to determine which projects to undertake

  With this background, we’re ready to solve the software project selection problem. As always with a Solver model, we begin by identifying our target cell, the changing cells, and the constraints.

  • Target cell. We maximize the NPV generated by selected projects.

  • Changing cells. We look for a 0 or 1 binary changing cell for each project. I’ve located these cells in the range A6:A25 (and named the range doit). For example, a 1 in cell A6 indicates that we undertake Project 1; a 0 in cell C6 indicates that we don’t undertake Project 1.

  • Constraints. We need to ensure that for each Year t (t=1, 2, 3), Year t capital used is less than or equal to Year t capital available, and Year t labor used is less than or equal to Year t labor available.

  As you can see, our worksheet must compute for any selection of projects the NPV, the capital used annually, and the programmers used each year. In cell B2, I use the formula SUMPRODUCT(doit,NPV) to compute the total NPV generated by selected projects. (The range name NPV refers to the range C6:C25.) For every project with a 1 in column A, this formula picks up the NPV of the project, and for every project with a 0 in column A, this formula does not pick up the NPV of the project. Therefore, we’re able to compute the NPV of all projects, and our target cell is linear because it is computed by summing terms that follow the form (changing cell)*(constant). In a similar fashion, I compute the capital used each year and the labor used each year by copying from E2 to F2:J2 the formula SUMPRODUCT(doit,E6:E25).

• I now fill in the Solver Parameters dialog box as shown in Figure 30-2.

  
  Figure 30-2: Solver Parameters dialog box set up for the project selection model

  Our goal is to maximize NPV of selected projects (cell B2). Our changing cells (the range named doit) are the binary changing cells for each project. The constraint E2:J2<=E4:J4 ensures that during each year the capital and labor used are less than or equal to the capital and labor available. To add the constraint that makes the changing cells binary, I click Add in the Solver Parameters dialog box and then select Bin from the list in the middle of the dialog box. The Add Constraint dialog box should appear as shown in Figure 30-3.

  
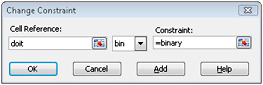
  Figure 30-3: Use the Bin option in the Add Constraint dialog box to set up binary changing cells-cells that will display either a 0 or a 1.

• Our model is linear because the target cell is computed as the sum of terms that have the form (changing cell)*(constant) and because the resource usage constraints are computed by comparing the sum of (changing cells)*(constants) to a constant.

• With the Solver Parameters dialog box filled in, click Solve and we have the results shown earlier in Figure 30-1. The company can obtain a maximum NPV of $9,293 million ($9.293 billion) by choosing Projects 2, 3, 6–10, 14–16, 19, and 20.