Tool 184: Standard Deviation

AKA

N/A

Classification

Analyzing/Trending (AT)

Tool description

The standard deviation is a powerful building block to perform descriptive and inferential statistics in research, project management, quality assurance, education and training, and many other disciplines. Used in many statistical formulae, it assists in the understanding of variability in data distributions. Considered a unit of measurement, a smaller standard deviation simply states that the data distribution is more homogeneous or has less variance.

Typical application

• To identify the extent of variability in a data set.

• To assist in statistical analyses such as process capability, analysis of variance (anova), design of experiments, and others.

• To compare two or more data distributions.

Problem-solving phase

	Select and define problem or opportunity
→	Identify and analyze causes or potential change
	Develop and plan possible solutions or change
	Implement and evaluate solution or change
→	Measure and report solution or change results
	Recognize and reward team efforts

Typically used by

1	Research/statistics
	Creativity/innovation
2	Engineering
	Project management
3	Manufacturing
4	Marketing/sales
	Administration/documentation
	Servicing/support
	Customer/quality metrics
5	Change management

links to other tools

before

• Data Collection Strategy

• Observation

• Questionnaires

• Surveying

• Frequency Distribution (FD)

after

• Process Capability Ratios

• Correlation Analysis

• Normal Probability Distribution

• Control Chart

• Analysis of Variance

Notes and key points

• Definition: The standard deviation is a measure of variability within a population or a sample of data. A more technical definition describes the standard deviation as the square root of the average of the squared deviations of the observations from the mean

  

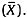
• Normal probability distribution

  

• Also refer to tool 119, normal probability distribution, in this handbook.

Step-by-step procedure

• STEP 1 First, collected scores are sequenced from the lowest to the highest score and placed into a table. See example Calculating the Standard Deviation—Test Scores.

• STEP 2 Calculate the mean 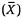and subtract from all scores.

• STEP 3 Check that the sum of - and + deviation scores (x) = 0.

• STEP 4 Square deviation scores and total.

• STEP 5 Calculate the variance (S²). Remember, use n-1 is total scores are less than 30.

• STEP 6 Take the square root of the variance to get the standard deviation.

Example of tool application

Calculating the Standard Deviation—Test Scores