| An arithmetic parser has no need of a target because you can accumulate a result of recognizing an assembly by working on the assembly's stack. The key design idea, then, is to produce the right number on an assembly's stack. First, when the parser sees a number with Num , the Num terminal places a token on the stack. The arithmetic parser must replace this token with its Double value, and to perform this task it needs an assembler. The parser also needs an assembler for each of the five operators. For example, after seeing ( '+' term ), the parser must perform an addition. To see where assemblers plug in to subparsers, it helps to write each operator on a separate line, as follows : expression = term (plusTerm minusTerm)*; term = factor (timesFactor divideFactor)*; plusTerm = '+' term; minusTerm = '-' term; factor = phrase expFactor phrase; timesFactor = '*' factor; divideFactor = '/' factor; expFactor = '^' factor; phrase = '(' expression ')' Num; The plusTerm parser must pop two terms and push their sum. The minusTerm parser must pop two terms and push their difference. Similarly, timesFactor , divideFactor , and expFactor must pop two terms and push their product, quotient , or exponentiation, respectively. Figure 7.1 shows the assembler classes that ArithmeticParser uses as it builds a value. Figure 7.1. The arithmetic package. This package contains classes that collaborate to create an arithmetic value from text. 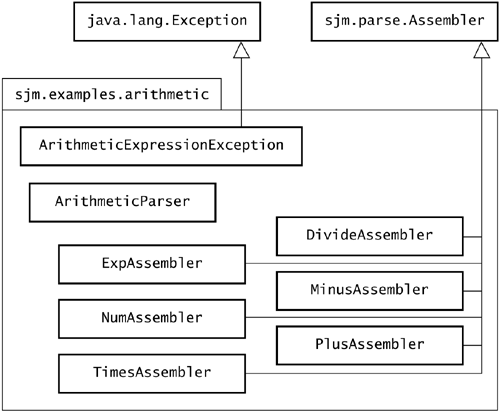 Figure 7.2 shows where the assemblers plug in to the subparsers of the ArithmeticParser class. Figure 7.2. Arithmetic parser assembler placement. This table shows the assembler that each arithmetic subparser employs. 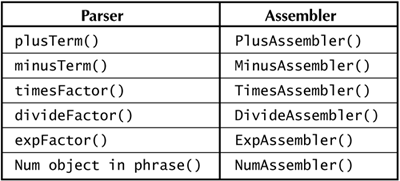 7.3.1 Assembler Code The phrase parser recognizes numbers using an object of class Num , which places a Token on the assembly's stack. Like all subclasses of Terminal that expect an assembly to return tokens, by default Num places the Token object it recognizes onto the assembly's stack. The design of our arithmetic parser calls for Double values, and not Tokens , to appear on the stack. When phrase sees a number, it asks its Num subparser to replace the Token with a corresponding Double . It accomplishes this with a NumAssembler : package sjm.examples.arithmetic; import sjm.parse.*; import sjm.parse.tokens.*; public class NumAssembler extends Assembler { /** * Replace the top token in the stack with the token's * Double value. */ public void workOn(Assembly a) { Token t = (Token) a.pop(); a.push(new Double(t.nval())); } } The remaining assemblers plug in after seeing an operator and a term or factor . These assemblers can assume that there are two numbers on the stack. For example, from the grammar rules the parser knows that the first time it recognizes a plusTerm , a term has immediately preceded it. Both the value of the preceding term and the value of the term in plusTerm will be on the stack. The job of PlusAssembler is to replace these values with their sum. Here is the code for PlusAssembler : package sjm.examples.arithmetic; import sjm.parse.*; public class PlusAssembler extends Assembler { /** * Pop two numbers from the stack and push their sum. */ public void workOn(Assembly a) { Double d1 = (Double) a.pop(); Double d2 = (Double) a.pop(); Double d3 = new Double(d2.doubleValue() + d1.doubleValue()); a.push(d3); } } The implementations of workOn() in classes MinusAssembler , TimesAssembler , DivideAssembler , and ExpAssembler differ only in which operator they apply to the two numbers on the stack. |