Sampling Test Cases

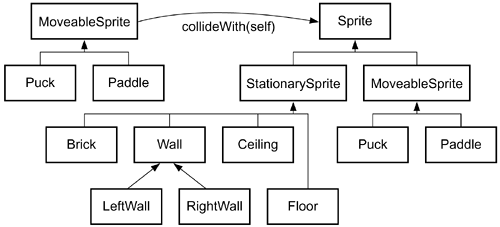
Exhaustive testing that is, running every possible test case covering every combination of values is obviously a reliable testing approach. However, in many situations the number of test cases is too large to handle reasonably. If there are more possible test cases than there is time to construct and execute them, a systematic technique is needed for determining which ones to actually use. If we have a choice then we would prefer to select the ones that will find the faults in which we are most interested. If we have no prior information, then a random selection is probably as good as we can do. In this section we will consider the general concept of sampling, and then we will apply it to interaction testing.

With any testing approach we are interested in ways that the level of coverage can be increased systematically. If a tester simply creates test cases without sufficient analysis, then creating more cases later often repeats some of the functionality already tested. With the techniques presented here, there is a well-defined set of cases and a well-defined technique for increasing coverage.

There are a number of possibilities for determining which test cases to select. The technique we will discuss first uses a simple selection process based on a probability distribution. A probability distribution defines, for each data value in a population, a set of allowable values, and the probability that value will be selected. Under a uniform probability distribution, each value in the population is assigned the same selection probability.

We define the population of interest to be all possible test cases that could be executed. This includes all preconditions and all possible combinations of input values. A sample is a subset of a population that has been selected based on some probability distribution. One approach is to base the probability distribution on the user profile. If the uses of the system are ranked by frequency, the ranks can be transformed into probabilities. The higher the frequency of use, the larger the probability of selection. But more about this later (see Use Profile on page 313).

We can select a stratified sample in which tests are selected from a series of categories. A stratified sample is a set of samples in which each sample represents a specific subpopulation for example, we might select test cases that we are certain exercise each component of the architecture. A population of tests is divided into subsets so that a subset contains all of the tests that exercise a specific component. Sampling occurs on each subset independent of the others.

An approach that works well is to use the actors from the use case model as the basis for stratifying the test cases. That is, we select a sample of test cases from the uses of each actor. Each actor uses some subset of the possible uses with some frequency (see Use Profiles, on page 130). Stratifying the test case samples by each actor provides an effective means of increasing the reliability of the system. Running the selected tests uses the system the way that it will be used in typical situations and finds those defects that are most likely to be found in typical use. Removing these defects produces the largest possible increases in reliability with the smallest effort.

The sampling technique provides an algorithm for selecting a test suite from a set of possible test cases. This does not mandate how the population of test cases is determined in the first place. The test process is intended to define the population of tests in which we are interested for example, functional test cases and then to define a technique for selecting which of these test cases will be constructed and executed.

A test suite for a component may be constructed using a combination of techniques. Consider the Velocity class we used in Chapter 5 in which we did an exhaustive test of direction values, but only a few speed values. We can reduce the number of tests by first using the specification as a source of test cases, and then applying a sampling technique to supplement those tests.

The specification of Velocity includes a modifier operation called setDirection(const Direction &newDirection) whose precondition requires newDirection to be in the range 0 through 359, inclusive. The postcondition specifies that the receiver's direction has been modified to the value of newDirection. We first generate test data for this method using the specification as a basis. First, note that Direction is a typedef for int so we are selecting from the set of integers rather than a set of objects. Rather than sample for every test case (0 through 359), we first select values based on boundary values. So we can have three tests around the boundary of zero, perhaps -1, 0, and 1. If this were a "design by contract" project, the -1 value would not be a legitimate test case. There should be a similar set of values around the other boundary, so perhaps 358, 359, and 360. Again, 360 is not legitimate in a contract context. There should be tests in the intervals between 1 and 358 and here is where sampling plays a useful role. The values in the two intervals could be sampled using something like int(random() * 360) and int(-1 * random() * 360). The random() function generates a pseudo random value between 0.0 and 1.0 in accordance with a uniform distribution, so each value is within the interval and each value has an equal chance of being selected.

The advantage of using the random value generator in the test case is that over iterations and reapplications of test cases, many values in the intervals will be tested rather than the same ones over time. The disadvantage is that now the test cases are not being reproduced since a different value is used every time. By having the test driver record the generated values as part of the test log, we can re-create any failed test case. Any randomly chosen value that causes a failure is explicitly added to the test suite and is used to test the repaired software. After the fault has been repaired, those values can be used to validate the repair. The regression suite consists mainly of those tests that originally produced failures but were ultimately passed by the software.

Now let us consider the interaction between two classes: Sprite and MoveableSprite in the collideInto() operation (see Figure 6.5). Both Sprite and MoveableSprite classes are abstract, so we have an opportunity to design tests that can be reused by their subclasses. The precondition places no restriction on the parameter so we need to find some other way to determine the population from which we will sample. There are three dimensions along which we can sample.

Figure 6.5. Specification for operation collideInto()

First, Sprite is the base class in a very large class family, which is a set of classes related by inheritance. An object from any one of the classes in the family can be substituted for the sprite parameter. Therefore, we should sample from this set for possible parameters. This is one of the problems we mentioned earlier about testing object-oriented systems. At some time in the future, a new member of the family can be created and passed to this routine without any recompilation of the MoveableSprite class. Traditional techniques for triggering regression tests do not work in this environment. They should be controlled in the configuration management tool or perhaps the development environment. Each new class definition stimulates a round of regression testing. Usually however only the overridden methods will need to be tested if most of the methods are inherited.

Tip

Use the class diagram to identify the classes that should be involved in a regression test resulting from the creation of a new class. Examine the parent classes for this new class and identify interactions in which those classes participate. Execute the tests that interact those parents with other classes, but substitute the new class for the parent class in the test.

The second dimension for sampling is to consider that each member of the family may have different states that can cause two objects from the same class to behave differently. Obviously the Puck and Wall classes probably have some interesting differences in their states. In the case of families of classes, the state machines are related along the lines of the inheritance hierarchy. Our experience and a number of published papers have shown that as we look down the inheritance hierarchy, there will be the same number of states or more states in the derived class as there are in the base class. We should cover the states defined for each class with special emphasis on the new states added at that level in the inheritance hierarchy.

A third dimension relates to the class family associated with MoveableSprite. This is a subset of the Sprite family. Once these tests are designed, they can be applied to any of the classes in the family, assuming the substitution principle has been followed during design.

Given these three dimensions, we have the possibility of a combinatorial explosion in the number of test configurations. In this scenario, a test case would have a member of the MoveableSprite family sending a message to a member of the Sprite family, which may be in any one of its states.

Orthogonal Array Testing

Orthogonal arrays provide a specific sampling technique that seeks to limit the explosion by defining pair-wise combinations of a set of interacting objects. Most of the faults resulting from interactions are due to two-way interactions. One specific technique for selecting a sample is orthogonal array testing system (OATS). An orthogonal array is an array of values in which each column represents a factor, which is a variable in an experiment. In our case it will represent a specific class family^[5] in the software system. Each variable can take on a certain set of values called levels. In our testing work, each level will be a specific class in the family. There will also be a parallel factor and set of levels that correspond to the states of these classes. The value entered into a particular cell in the array is an instance of the specific class or is a specific state of an object.

^[5] A class family is a class and all of the classes that inherit from that class.

Figure 6.6. Explosion of test cases

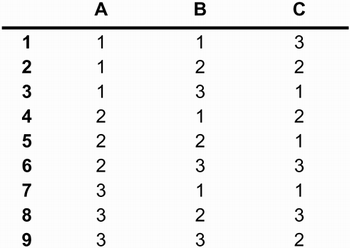
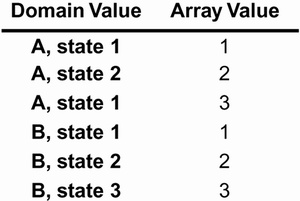
In an orthogonal array, the factors are combined pair-wise rather than representing all possible combinations of the levels for the factors. For example, suppose that we have three factors say, A, B, and C each with three levels say, 1, 2, and 3. There are 27 possible combinations of these values 3 for A times the 3 for B times the 3 for C. If pair-wise combinations are used instead that is, if we consider only those combinations in which a given level appears exactly twice then there are only 9 combinations as shown in Figure 6.7.

Figure 6.7. Pair-wise combinations of three factors that have three levels each

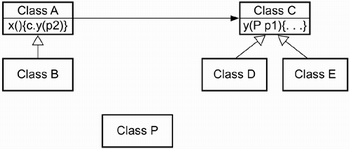
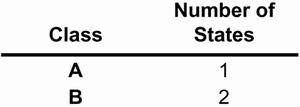
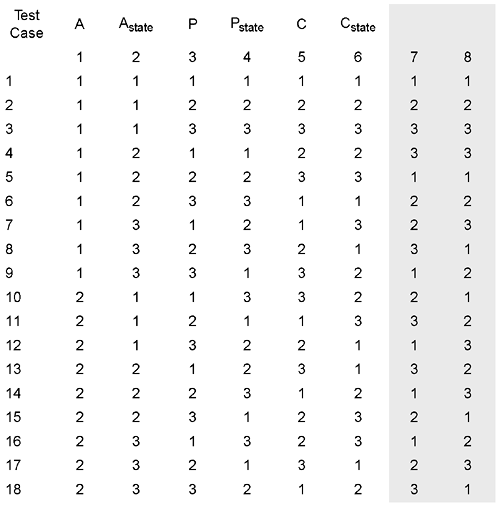
OATS uses a balanced design. Every level of a factor will appear exactly the same number of times as every other level of that factor. If we think of the rows of a table as test cases, then 18 of the possible 27 tests are not being conducted. This is a systematic way of reducing the number of test cases. If we later decide that additional tests should be run, we will know exactly which combinations have not been tested. This is also a logical way of doing the reduction. Most of the errors that are encountered are between pairs of objects rather than among several objects. In this way, we are testing those situations that are most likely to reveal faults. To demonstrate OATS, we will work through a general example and then a Brickles-specific example. The general example comprises interactions between senders in a class family A, receivers in a class family C, and parameters in a class family P (see Figure 6.8). Each class has a state transition diagram associated with it. The details are not important. The number of states that we are assuming each class has is shown in Figure 6.9.

Figure 6.8. A general example of applying OATS

Figure 6.9. The number of states associated with classes in the general OATS example

The major activity in this technique is to map the problem of testing the interaction of two inheritance hierarchies with respect to a parameter object. To identify test cases using orthogonal arrays, observe the following five steps:

Step 1. Identify all factors. The sending hierarchy is one factor. The receiving hierarchy is a second factor. There is also a factor associated with each parameter position in the message. There is an additional factor associated with each class factor namely, the states associated with instances of the class. This experiment (see Figure 6.8) has six factors: the class A hierarchy, the class P hierarchy, and the class C hierarchy and factors for the states associated with each class hierarchy.

Step 2. Determine levels for each factor. The levels for each factor are determined by considering the set of possible values.

• One factor has one level: the parameter class family only has one member: P.

• Two factors have a maximum of two levels; the sending class family has two members: A and B; the maximum number of states for a class in the P family is two.

• Three factors have a maximum of three levels: the receiving family has three members, and the maximum number of states for a class in the A family and in the C family is three.

Step 3. Locate a standard orthogonal array that fits the problem. Given our need for six factors of, at most, three levels, we turn to the tables of pre-computed arrays called standard arrays [Phadke89]. The notation 2¹ x 3⁷ for L₁₈ (see Figure 6.16) indicates that the array addresses one factor with two levels and seven factors with three levels. L₁₈ is the smallest standard array that will fit the problem. A standard array can be larger than a problem, but not smaller.^[6]

^[6] Use a larger array if the number of levels is likely to change in the future for example, if more subclasses might be added to a receiving class family. Using a larger array allows for future expansion of test cases when levels are added.

Figure 6.16. The standard orthogonal array L₁₈ (2¹ x 3⁷)

Step 4. Establish a mapping from each factor onto the integers in the array so that the standard array can be interpreted. Standard array entries are integer values. We analyze each factor in the following list.

• For the sender class family there are two classes, A and B, so the first column in L₁₈ can be used to represent this data (Figure 6.10). We adopt an encoding in which a value of 1 in the first column of the array corresponds to the A class and a value of 2 corresponds to the B class.

  Figure 6.10. Class A hierarchy

  

• Class A has two states and class B has three states. When there is a difference in the number of levels, we can use a column that matches or exceeds the maximum. The second column in L₁₈ has a maximum of three, which will fit this data. The interpretation of the values in the second column depends on the values in the first column. For a value of 2 (class B) in the first column, we are representing the states of class B in the second column. If the value in the first column is 1, then the second column represents the states of class A. In Figure 6.11, the state values for class B directly correspond to the integer values in the column. Since class A only has two states, how do we interpret a 3 in the second column when there is a value of 1 (class A) in the first column? We interpret it as though it were either 1 or 2. When a value in the column does not properly correspond to values in other columns, then we interpret it as some other domain value that is repeated. In this case, as denoted in the table, 3 in the array will correspond to state 1. The interpretation can be arbitrary or based on an observation that an instance of A is more likely to be in state "1" or there is a higher risk associated with being in state "1."

  Figure 6.11. States for class A hierarchy

  

• The third column in L₁₈ represents the parameter hierarchy that only has one class, P. Any value in the third column represents P (Figure 6.12).

  Figure 6.12. States for the class P hierarchy

  

• The fourth column represents the states of P, of which there are two (Figure 6.13). However, the column has values 1, 2, and 3. An array value of 1 corresponds to state 1, a value of 2 corresponds to state 2 of the P class, and a value of 3 will repeat state 2 of class P.

  Figure 6.13. States for class P hierarchy

  

• The fifth column represents the class C hierarchy, which has three members. There is a direct correspondence between classes and the integer values in the array. The interpretation is shown in Figure 6.14.

  Figure 6.14. The C Class hierarchy

  

• The sixth column represents the states of the C, D, and E classes (Figure 6.15). Since C has only 2 states, the array value of 3 will correspond to a value of 2. For classes D and E, there is a direct correspondence between states and array values.

  Figure 6.15. States for class P hierarchy

  

Note: the last two columns of L₁₈ are not used.

Step 5. Construct test cases based on the mapping and the rows in the table.

Each row in the orthogonal array, Figure 6.16, specifies one specific test case. The orthogonal array is interpreted back into test cases by decoding the level numbers for a row in the array back to the individual lists for each factor. Thus, for example, the 10th row of L₁₈ is interpreted as test case number 10 in which an instance of class B in state 1 is to send the message by passing an instance of class P in state 3 to an instance of class E in state 2. The last two values in the row are ignored since we did not use those factors.

Adequacy Criteria for OATS

One of the useful things about OATS is the ability to vary how completely the software under test is covered. Here are some possible levels that can be used:

• Exhaustive All possible combinations of all factors are considered. Lots of confidence, lots of expense.

• Minimal Only the interactions between the base classes from each hierarchy are tested. Little confidence from few test cases.

• Random The tester haphazardly selects cases from several of the classes. Confidence level unclear, number of test cases arbitrary. Not a statistically random sample.

• Representative A uniform sample that ensures that every class is tested to some level. Confidence level is the same across classes; number of test cases is minimized.

• Weighted Representative Adds cases to the representative approach based on relative importance or risk associated with the class. This is the approach we have illustrated in this section. At any point where the matrix has more levels than the actual problem does, the tester has the opportunity to generate additional tests for priority levels of factors.

Once all the test cases have been run, look at the results to see if failure can be associated with one or more specific factor levels for example, perhaps most of the test cases associated with instances of class A, state 2 fail. This information is useful for developers to track down bugs, and it is useful for testers to indicate that additional test cases might be warranted.

Another Example

Now let us return to the MoveableSprite::collideInto() example from page 227. A MoveableSprite object may be passed to any Sprite object when it is sent the collideInto() message. In the present design, the Sprite class family includes MoveableSprite, StationarySprite, Puck, Paddle, Brick, Wall, RightWall, LeftWall, Floor, and Ceiling.

We make the following analysis and observations:

1. Classes Sprite, MoveableSprite, StationarySprite, and Wall are abstract classes. We will talk about how to test abstract classes in the next chapter, but for now, they will not be a part of the OATS scenario.

2. Only Puck and Paddle are derived from MoveableSprite, so only MoveableSprite, Puck, and Paddle can receive the collideInto() message. However, all the classes derived from Sprite can receive the collideWith() message.

3. Each of the objects passed as a parameter is in a specific state. The objects may behave differently in different states. An instance of MoveableSprite may be moving or not. If it is moving, then it is moving in a specific direction. From a state perspective, the directions can be grouped into states named DueNorth, DueSouth, DueEast, DueWest, NorthEast, NorthWest, SouthEast, and SouthWest. Note that an instance of Paddle can only move DueEast and DueWest.

4. In this case, the sender object and the parameter object are the same, so there are only two class family columns and two state of classes columns.

The possible values for each attribute of the test case are shown in Figure 6.17.

Figure 6.17. Test attribute values

If we tested all possible combinations, the number of possible tests is 2 x 9 x 8 x 9 = 1296. Some of these can be eliminated because nonmoveable sprites do not have the direction states. The total now appears to be 2 x 9 x 2 x 9 + 2 x 9 x 6 x 1, = 432 test cases still quite a few. By using OATS, we can further reduce the number of test cases and still be effective. For example, these are the selected combinations from Figure 6.17:

1. Paddle, DueEast, Puck, SouthEast

2. Paddle, DueEast, Puck, NorthEast

3. Paddle, DueEast, Puck, NorthWest

4. Paddle, DueEast, Puck, DueWest

5. Puck, DueEast, Puck, DueWest

OATS would allow case #4 to be eliminated because in #3 Paddle is tested while moving DueEast; in #5 Puck is tested moving DueWest; in #3 Paddle is tested colliding with Puck. The complete OATS analysis would reduce considerably the number of tests required.

Another Application of OATS

Consider the need to test a collection class such as Stack, in which the class is implemented as a C++ template (see Figure 6.18).

Figure 6.18. A C++ class template for Stack

The developer's intention is for template parameter T to be replaced by any class when Stack is instantiated. Obviously, we cannot test the Stack class definition with all possible substitutions. The Stack, like any collection class, does not invoke any methods on the objects that it contains. Therefore, the interface implemented by the parameter class does not matter.

To test the template code, we would select a stratified sample of classes from all of the classes that are available including vendor libraries, language libraries, and application code. Depending on the exact programming language used and other factors, the categories in the stratification will include the amount of memory used by each instance, the number of associations, and whether the objects placed in a collection are persistent. Then we would select a subset of this set of classes each time a collection class needs to be tested. This second sampling can be guided by OATS.

For more complex templates, sets of possible substitutes for each parameter are created. Then OATS creates tests that involve combinations of parameter substitutions. These tests provide the maximum search for interactions among the parameters with the minimum number of tests.