Hack 33. Predict the Length of a Lifetime
| Many of us instinctively trust that things that have been around a long time are likely to be around a lot longer, and things that haven't, aren't. The formalization of this heuristic is known as Gott's Principle, and the math is easy to do. Physicist J. Richard Gott III has so far correctly predicted when the Berlin Wall would fall and calculated the duration of 44 Broadway shows.1 Controversially, he has predicted that the human race will probably exist between 5,100 and 7.8 million more years, but no longer. He argues that this is a good reason to create self-sustaining space colonies: if the human race puts some eggs in other nests, we might extend the life span of our species in case of an asteroid strike or nuclear war on the home planet.2 Gott believes that his simple calculations can be extended to almost anything at all, within certain parameters. To predict how long something will be around by using these calculations, all you need to know is how long it has been around already. In ActionGott bases his calculations on what he calls the Copernican Principle (and what some people call, in this specific application, Gott's Principle). The principle says that when you choose a moment in time to calculate the lifetime of a phenomenon, that moment is probably quite ordinary, not special or privileged, just as Copernicus told us the Earth does not occupy a privileged place in the universe. It's important to choose subjects at ordinary, unprivileged moments. Biasing your test by choosing subjects that you already believe to be near the beginning or end of their life spansuch as the human occupants of a neonatal ward or a nursing homewill yield bad results. Further, Gott's Principle is less useful in situations where actuarial data already exists. Plenty of actuarial data is available on the human life span already, so Gott's Principle is less useful here. Having chosen a moment, let's examine it. All else being equal, there's a 50 percent chance the moment is somewhere in the middle 50 percent of the phenomenon's lifetime, a 60 percent chance it's in the middle 60 percent, a 95 percent chance it's in the middle 95 percent, and so on. Therefore, there's only a 25 percent chance that you've chosen a moment in the first fourth of its lifetime, a 20 percent chance it's in the first fifth, a 2.5 percent chance it's in the last 2.5 percent of the subject's lifetime, and so on. Table 3-11 provides equations for the 50 percent, 60 percent, and 95 percent confidence levels. The variable tpast represents how long the object has existed, and tfuture represents how long it is expected to continue.
Let's look at a simple example. Quick: whose work do you think is more likely to be listened to 50 years from now, Johann Sebastian Bach's or Britney Spears'? Bach's first work was performed around 1705. At the time of this writing, that's 300 years ago. Britney Spears' first album was released in January 1999, about 6.5 years or 79 months ago. Consulting Table 3-11, for the 60 percent confidence level, we see that the minimum tfuture is tpast/4, and the maximum is 4tpast. Since tpast for Britney's music is 79 months, there is a 60 percent chance that Britney's music will be heard for between 79/4 months and 79x4 months longer. In other words, we can be 60 percent sure that Britney will be a cultural force for somewhere between 19.75 months (1.6 years) and 316 months (26.3 years) from now.
By the same token, we can expect people to listen to Bach's music for somewhere between another 300/4 and 300x4 years at the 60 percent confidence level, or somewhere between 75 years and 1,200 years from now. Thus, we can predict that there's a good chance that Britney's music will die with her fans, and there's a good chance that Bach will be listened to in the fourth millennium. How It WorksSuppose we are studying the lifetime of some object that we'll call the target. As we've already seen, there's a 60 percent chance we are somewhere in the middle 60 percent of the object's lifetime (Figure 3-4).3 Figure 3-4. The middle 60 percent of the lifetime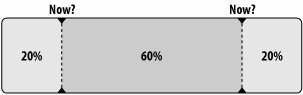 If we are at the very end of this middle 60 percent, we are at the second point marked "now?" in Figure 3-4. At this point, only 20 percent of the target's lifetime is remaining (Figure 3-5), which means that tfuture is equal to one-fourth of tpast (80 percent). This is the minimum remaining lifetime we expect at the 60 percent confidence level. Figure 3-5. The minimum remaining lifetime (60 percent confidence level) Similarly, if we are at the beginning of the middle 60 percent (the first point marked "now?" in Figure 3-4), 80 percent of the target's existence lies in the future, as depicted in Figure 3-6. Therefore, tfuture (80 percent) is equal to 4xtpast (20 percent). This is the maximum remaining lifetime we expect at the current confidence level. Figure 3-6. The maximum remaining lifetime (60 percent confidence level)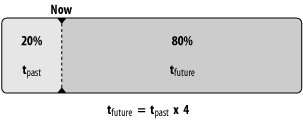 Since there's a 60 percent chance we're between these two points, we can calculate with 60 percent confidence that the future duration of the target (tfuture) is between tpast/4 and 4xtpast. In Real LifeSuppose you want to invest in a company and you want to estimate how long the company will be around to determine whether it's a good investment. You can use Gott's Principle to do so. Although it's not publicly traded, let's take O'Reilly Media, the publisher of this book, as an example.
According to the Wikipedia, O'Reilly started in 1978 as a consulting firm doing technical writing. It's July 2005 as I write this, so O'Reilly has existed as a company for approximately 27 years. How long can we expect O'Reilly to continue to exist? Here's O'Reilly's likely lifetime, calculated at the 50 percent confidence level:
Here are our expectations at the 60 percent confidence level:
Finally, here's our prediction with 95 percent confidence:
In the post-dot-com economy, these figures look pretty good. For example, Apple Computer's aren't much better, and Microsoft was founded in 1975, so the same can be said for it. A real investor would want to consider many other factors, such as annual revenue and stock price, but as a first cut, it looks as though O'Reilly Media is at least as likely to outlive a hypothetical investor as to tank in the next decade. Endnotes
Ron Hale-Evans |
EAN: 2147483647
Pages: 114
