3.3 Conditioning with Sets of Probabilities

Suppose that an agent's uncertainty is defined in terms of a set of probability measures. If the agent observes U, the obvious thing to do is to condition each member of on U. This suggests that after observing U, the agent's uncertainty should be represented by the set {μ|U: μ ∊ }. There is one obvious issue that needs to be addressed: What happens if μ(U) = 0 for some μ ∊ ? There are two choices here: either to say that conditioning makes sense only if μ(U) > 0 for all μ ∊ (i.e., if _*U) > 0) or to consider only those measures μ for which μ(U) > 0. The latter choice is somewhat more general, so that is what I use here. Thus, I define

(Note that if the uncertainty in this case is represented using the sample space W, as discussed in Section 2.3, then what is going on here is that, just as in Section 3.1, all worlds incompatible with the observation are eliminated. However, now the set of worlds incompatible with observation U consists of all pairs (μ, w) such that either μ(U) = 0 or w ∉ U.)

Once the agent has a set | U of conditional probability measures, it is possible to consider lower and upper conditional probabilities. However, this is not the only way to represent the update of a set of probability measures. In particular, it is also possible to consider updating the plausibility measure Pl discussed in Section 2.8. This is done in Section 3.9, where there is a general discussion of updating plausibility measures. For now, I just consider how sets of probabilities can be used to deal with the three-prisoners puzzle.

Example 3.3.1

The three-prisoners puzzle is an old chestnut that is somewhat similar in spirit to the second-ace puzzle discussed in Chapter 1, although it illustrates somewhat different issues.

Of three prisoners a, b, and c, two are to be executed, but a does not know which. He therefore says to the jailer, "Since either b or c is certainly going to be executed, you will give me no information about my own chances if you give me the name of one man, either b or c, who is going to be executed." Accepting this argument, the jailer truthfully replies, "b will be executed." Thereupon a feels happier because before the jailer replied, his own chance of execution was 2/3, but afterward there are only two people, himself and c, who could be the one not executed, and so his chance of execution is 1/2.

Note that in order for a to believe that his own chance of execution was 2/3 before the jailer replied, he seems to be implicitly assuming the principle of indifference. A straightforward application of the principle of indifference also seems to lead to a's believing that his chances of execution goes down to 1/2 after hearing the jailer's statement. Yet it seems that the jailer did not give him any new relevant information. Is a justified in believing that his chances of avoiding execution have improved? If so, it seems that a would be equally justified in believing that his chances of avoiding execution would have improved if the jailer had said "c will be executed." It seems that a's prospects improve no matter what the jailer says! That does not seem quite right.

The principle of indifference is implicitly being applied here to a space consisting of three worlds—say w_a, w_b, and w_c—where in world w_x, prisoner x is pardoned. But this representation of a world does not take into account what the jailer says. Perhaps a better representation of a possible situation is as a pair (x, y), where x, y ∈{a, b, c}. Intuitively, a pair (x, y) represents a situation where x is pardoned and the jailer says that y will be executed in response to a's question. Since the jailer answers truthfully, x ≠ y; since the jailer will never tell a directly that a will be executed, y ≠ a. Thus, the set of possible worlds is {(a, b), (a, c), (b, c), (c, b)}. The event lives -a—a lives—corresponds to the set {(a, b), (a, c)}. Similarly, the events lives -b and lives -c correspond to the sets {(b, c)} and {(c, b)}, respectively. Assume in accord with the principle of indifference that each prisoner is equally likely to be pardoned, so that each of these three events has probability 1/3.

The event says-b—the jailer says b—corresponds to the set {(a, b), (c, b)}; the story does not give a probability for this event. To do standard probabilistic conditioning, this set must be measurable and have a probability. The event {(c, b)} (lives-c) has probability 1/3. But what is the probability of {(a, b)}? That depends on the jailer's strategy in the one case where he has a choice, namely, when a lives. He gets to choose between saying b and c in that case. The probability of (a, b) depends on the probability that he says b if a lives; that is, μ(says-b | lives-a).

If the jailer applies the principle of indifference in choosing between saying b and c if a is pardoned, so that μ(says-b | lives-a) = 1/2, then μ({(a, b)}) = μ({(a, c)}) = 1/6, and μ(says-b) = 1/2. With this assumption,

Thus, if μ(says-b) = 1/2, the jailer's answer does not affect a's probability.

Suppose more generally that μ_α, 0 ≤ α ≤ 1, is the probability measure such that μ_α(lives-a) = μ_α(lives-b) = μ_α(lives-c) = 1/3 and μ_α(says-b | lives-a) = α. Then straightforward computations show that

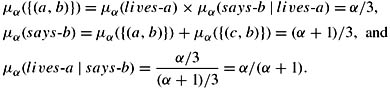
Thus, μ_1/2 = μ. Moreover, if α ≠ 1/2 (i.e., if the jailer had a particular preference for answering either b or c when a was the one pardoned), then a's probability of being executed would change, depending on the answer. For example, if α = 0, then if a is pardoned, the jailer will definitely say c. Thus, if the jailer actually says b, then a knows that he is definitely not pardoned, that is, μ₀(lives-a | says-b) = 0. Similarly, if α = 1, then a knows that if either he or c is pardoned, then the jailer will say b, while if b is pardoned the jailer will say c. Given that the jailer says b, from a's point of view the one pardoned is equally likely to be him or c; thus, μ₁(lives-a | says-b) = 1/2. In fact, it is easy to see that if _J = {μ_α: α ∊ [0,1]}, then (_J | says-b)*(lives-a) = 0 and _J | says-b)*(lives-a) = 1/2.

To summarize, the intuitive answer—that the jailer's answer gives a no information—is correct if the jailer applies the principle of indifference in the one case where he has a choice in what to say, namely, when a is actually the one to live. If the jailer does not apply the principle of indifference in this case, then a may gain information. On the other hand, if a does not know what strategy the jailer is using to answer (and is not willing to place a probability on these strategies), then his prior point probability of 1/3 "diffuses" to an interval.