A Brief Overview of Digital Audio
| [ LiB ] |
A Brief Overview of Digital Audio
If analog recording helped bring the industry to where it is today, digital recording will help carry it until the next technological milestone. With computers and processing chips becoming more and more efficient in transforming information, audio developers saw the potential this new technology could offer. Fifty years later, digital audio has proven itself to be a great tool helping us with recording, restoration, creation, and editing.
If the quality of digital components in the late eighties and early nineties was not up to par with the high end analog technology, the new digital standards are promising much greater fidelity than even the best analog recorders . At this point, the advantage of digital audio is clear. And for those who miss the "analog feel," it is possible to marry the two technologies to achieve the best possible results.
Understanding how sound is transformed into digital audio will help your recording, editing, and mixing sessions. If you understand the process, you will be in a better position to predict and control the result. This will save you time and most likely produce better results.
Digital audio recordings, like analog audio recordings, are not all created equal. Recording with higher digital resolutions and superior equipment ( analog-to-digital converters) in conjunction with the technology available in Cubase SX/SL will allow you to create better-sounding results. Let's look at how this works and how digital recordings are different from analog recordings.
What Is Analog Sound?
When a musical instrument is played , it vibrates. Examples of this include the string of a violin, the skin of a drum, and even the cone of a loudspeaker. This vibration is transferred to the molecules of the air, which carry the sound to our ears. Receiving the sound, our eardrums vibrate, moving back and forth anywhere between 20 and 20,000 times every second. A sound's rate of vibration is called its frequency and is measured in hertz. (The human range of hearing is typically from 20 Hz to 20 kHz (kilohertz).) If the frequency of the vibration is slow, we hear a low note; if the frequency is fast, we hear a high note. If the vibration is gentle, making the air move back and forth only a little, we hear a soft sound. This movement is known as amplitude. If the amplitude is high, making the windows rattle, we hear a loud sound!
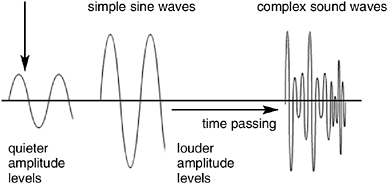
If you were to graph air movement against time, you could draw a picture of the sound. This is called a waveform . You can see a very simple waveform at low amplitude at left in Figure 1.4. The middle waveform is the same sound, but much louder (higher amplitude). Finally, the waveform on the right is a musical instrument, which contains harmonicsa wider range of simultaneous frequencies. In all of these waveforms, there is one constant: The horizontal axis always represents time and the vertical axis always represents amplitude.
Figure 1.4. The vertical axis represents the amplitude of a waveform and the horizontal axis represents time.
Real life sounds don't consist of just one frequency but of many frequencies mixed together at different levels of amplitude (loudness). This is what makes a musical sound interesting. Despite its complexity, a waveform can be represented by a graph. At any given time, the waveform has a measurable amplitude. If we can capture this "'picture'' and then reproduce it, we've succeeded in our goal of recording sound.
A gramophone record does this in an easily visible way. Set up a mechanism that transfers air vibration (sound) into the mechanical vibration of a steel needle. Let the needle draw the waveform onto a groove in tinfoil or wax. "'Read'' the wiggles in this groove with a similar needle. Amplify the vibration as best you can. Well done, Mr. Edison!
Instead of wiggles in a groove, you might decide to store the waveform as patterns of magnetism on recording tape. But either way, you're trying to draw an exact picture of the waveform. You're making an analog recording by using a continuous stream of information. This is different from digital audio recordings, as you will see later in this chapter.
The second dimension of sound is amplitude, or the intensity of molecule displacement. When many molecules are moved, the sound will be louder. Inversely, if few molecules are moved in space, the sound is softer. Amplitude is measured in volts , because this displacement of molecules creates energy. When the energy is positive, it pushes molecules forward, making the line in Figure 1.4 move upward. When the energy is negative, it pushes the molecules backwards , making the line go downward. When the line is near the center, it means that fewer molecules are being moved around. That's why the sound appears to be quieter.
Space is a third dimension to sound. This dimension does not have its own axis because it is usually the result of amplitude variations through time, but the space will affect the waveform itself. In other words, the space will affect the amplitude of a sound through time. This will be important when we talk about effects and microphone placement when recording or mixing digital audio. But suffice it to say now that the environment in which sound occurs has a great influence on how we will perceive the sound.
What Is Digital Audio?
Where analog sound is a continuous variation of the molecules of air traveling through space creating a sound's energy, the digital sound consists in a discretenoncontinuoussampling of this variation. In digital audio, there is no such thing as continuousonly the illusion of continuum.
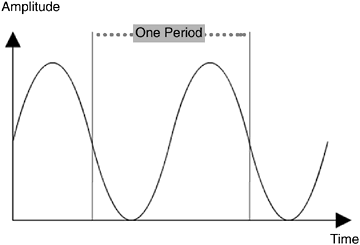
In 1928, mathematician Harry Nyquist developed a theory based on his finding that he could reproduce a waveform if he could sample the variation of sound at least twice in every period of that waveform. A period is a full cycle of the sound (see Figure 1.5) measured in hertz (this name was given in honor of Heinrich hertz, who developed another theory regarding the relation between sound cycles and their frequency in 1888). So, if you have a sound that has 20 Hz, you need at least 40 samples to reproduce it. The value captured by the sample is the voltage of that sound at a specific point in time. Obviously, in the 1920s, computers were not around to keep the large number of values needed to reproduce this theory adequately, but as you probably guessed, we do have this technology available now.
Figure 1.5. The bits in a digital recording will store a discrete amplitude value, and the frequency at which these amplitude values are stored in memory as they fluctuate through time is called the sampling frequency.
How Sampling Works
In the analog world, the amplitude is measured as a voltage value. In the digital world, this value is quantified and stored as a number. In the computer world, numbers are stored as binary memory units called bits. The more bits you have, the longer this number will be. Longer numbers are also synonymous with more precise representations of the original voltage values the digital audio was meant to store. In other words, every bit keeps the value of the amplitude (or voltage) as a binary number. The more bits you have, the more values you have. You may compare this with color depth in digital pictures. When you have eight bits of color, you have a 256- color palette, a 16-bit resolution yields over 65,000 colors, a 24-bit resolution offers over 16.7 million colors, and so on. In sound, colors are replaced by voltage values. The higher the resolution in bit depth, the smaller the increments are between these voltage values. If you were to calculate the distance between New York and Paris using the same accuracy as the one provided by a 24-bit digital recording system, you would be accurate within a foot (13.29 inches or 0.34 meter to be precise). That's an accuracy of 0.0000005%! It would be fair to assume that most high resolution digital audio systems are fairly accurate at reproducing amplitude variations of an audio signal.
This also means that the more increments you have, the less noise your amplifier will create as it moves from one value to another.
Because the computer cannot make the in-between values, it jumps from one value to the next, creating noise-like artifacts, also called digital distortion . This is not something you want in your sound. So, the more values you have to represent different amplitudes, the more closely your sound will resemble the original analog signal in terms of amplitude variation. Time (measured in hertz) is the frequency at which you capture and store these voltage values, or bits. Like amplitude (bits), the frequency greatly affects the quality of your sound. As mentioned earlier, Nyquist said that you needed two samples per period of the waveform to be able to reproduce it, which means that if you want to reproduce a sound of 100 Hz, or 100 vibrations per second, you need 200 samples. Recording the amplitude of a sound through time is called your sampling, and since it is done at a specific interval, it is referred to as a sampling frequency. Like the frequency of your sound, it is also measured in hertz. In reality, complex sounds and high frequencies require much higher sampling frequencies than the one mentioned above. Because most audio components, such as amplifiers and speakers , can reproduce sounds ranging from 20 Hz to 20 kHz, the sampling frequency standard for compact disc digital audio was fixed at 44.1 kHza little bit more than twice the highest frequency produced by your monitoring system.
The first thing you notice when you change the sampling rate of a sound is that with higher sampling rates (more samples) you get a sharper, crisper sound with better definition and fewer artifacts. With lower sampling rates (fewer samples) you get a duller, mushier, and less defined sound. Why is this? Well, since you need twice as many samples as there are frequencies in your sound, the higher the sampling frequency, the higher the harmonics will be; and that's where the sound qualities mentioned above are found. When you reduce the sampling rate, you also reduce the bandwidth captured by the digital audio recording system. If your sampling rate is too low, you not only lose harmonics but fundamentals as well. And this will change the tonal quality of the sound altogether.
Figure 1.6 shows two sampling formats. The one on the left uses less memory because it samples the sound less often than the one on the right and has fewer bits representing amplitude values. As a result, there will be fewer samples to store, and each sample will take up less space in memory. But, consequently, it will not represent the original file very well and will probably create artifacts that will render it unrecognizable. In the first set of two images on the top, you can see the analog sound displayed as a single line.
Figure 1.6. Low resolution/low sampling rate vs. high resolution/high sampling rate.
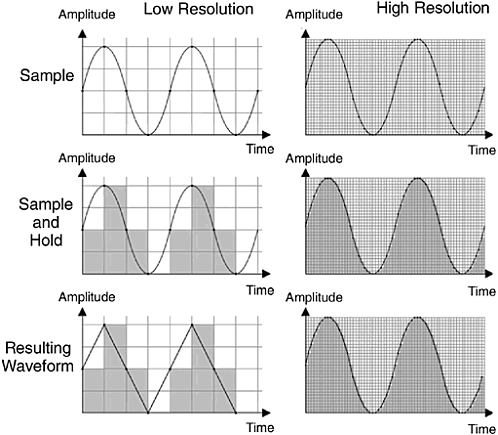
The center set of images demonstrates how the amplitude value of the sample is kept and held until the next sampled amplitude value is taken. As you can see in the right column, a more frequent sampling of amplitude values renders a much more accurate reproduction of the original waveform. If you look at the resulting waveform in the lower set of images, this becomes even more obvious when you look at the dark line representing the outline of the resulting waveform. The waveform on the right is closer to the original analog signal than the one on the left.
Sampling is simply the process of taking a snapshot of your sound through time. Every snapshot of your sound is kept and held until the next snapshot is taken. This process is called " Sample and Hold ." As mentioned earlier, the snapshot keeps the voltage value of the sound at a particular point in time. When playing back digital audio, an amplifier keeps the level of the recorded voltage value until the next sample. Before the sound is finally sent to the output, a certain amount of low-level noise is sometimes added to the process to hide the large gaps that may occur between voltage values, especially if you are using a low bit rate and low sampling rate for digital recording. This process is called dithering. Usually, this makes your sound smoother, but in low-resolution recordings (such as an 8-bit recording), it will add a certain amount of audible noise to your sound. If this dithering wasn't there, you might not hear noise, but your sound would contain more digital distortion.
So how does this tie into Cubase? Well, Cubase is, in many ways, a gigantic multitrack sampler, as it samples digital audio at various sampling rates and bit depths (or resolutions). Whenever you are recording an audio signal in a digital format, you are sampling this sound. Cubase will allow you to sample sound at rates of up to 96 kHz per second and at bit depths of up to 32 bits. How high you can go will, of course, depend on your audio hardware.
| [ LiB ] |