3.5 Shifts and Rotates

Another set of logical operations on bit strings are the shift and rotate operations. These functions can be further broken down into shift lefts, rotate lefts, shift rights, and rotate rights. These operations turn out to be very useful in many programs.

The shift left operation moves each bit in a bit string one position to the left, as shown in Figure 3-3. Bit zero moves into bit position one, the previous value in bit position one moves into bit position two, and so on.

Figure 3-3: Shift left operation (on a byte)

There are two questions that arise: 'What goes into bit zero?' and 'Where does the HO bit wind up?' We'll shift a zero into bit zero, and the previous value of the HO bit will be the carry out of this operation.

Several high-level languages (such as C/C++/C#, Java, and Delphi/Kylix) provide a shift left operator. In the C language family, this operator is < < . In Delphi/Kylix, you use the shl operator. Here are some examples:

 // C:          cLang = d << 1;    // Assigns d shifted left one position to                             // variable "cLang"  // Delphi:          Delphi := d shl 1; // Assigns d shifted left one position to                             // variable "Delphi"

Shifting the binary representation of a number one position to the left is equivalent to multiplying that value by two. Therefore, if you're using a programming language that doesn't provide an explicit shift left operator, you can usually simulate this by multiplying a binary integer value by two. Although the multiplication operation is usually slower than the shift left operation, most compilers are smart enough to translate a multiplication by a constant power of two into a shift left operation. Therefore, you could write code like the following in Visual Basic to do a shift left:

 vb = d * 2

A shift right operation is similar to a shift left, except we're moving the data in the opposite direction. Bit seven moves into bit six; bit six moves into bit five; bit five moves into bit four; and so on. During a shift right, we'll move azero into bit seven, and bit zero will be the carry out of the operation (see Figure 3-4). C, C++, C#, and Java use the > > operator for a shift right operation. Delphi/Kylix uses the shr operator. Most assembly languages also provide a shift right instruction ( shr on the 80x86).

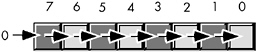
Figure 3-4: The shift right operation (on a byte)

Shifting an unsigned binary value right divides that value by two. For example, if you shift the unsigned representation of 254 ($FE) one place to the right, you get 127 ($7F), exactly as you would expect. However, if you shift the 8-bit two's complement binary representation of ˆ’ 2 ($FE) one position to the right, you get 127 ($7F), which is not correct. To divide a signed number by two using a shift, we must define a third shift operation: arithmetic shift right . An arithmetic shift right operation does not modify the value of the HO bit. Figure 3-5 shows the arithmetic shift right operation for an 8-bit operand.

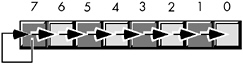
Figure 3-5: Arithmetic shift right operation (on a byte)

This generally produces the result you expect for two's complement signed operands. For example, if you perform the arithmetic shift right operation on ˆ’ 2 ($FE), you get ˆ’ 1 ($FF). Note, however, that this operation always rounds the numbers to the closest integer that is less than or equal to the actual result . If you arithmetically shift right ˆ’ 1 ($FF), the result is ˆ’ 1, not zero. Because ˆ’ 1 is less than zero, the arithmetic shift right operation rounds towards ˆ’ 1. This is not a 'bug' in the arithmetic shift right operation; it just uses a different (though valid) definition of integer division. The bottom line, however, is that you probably won't be able to use a signed division operator as a substitute for arithmetic shift right in languages that don't support arithmetic shift right, because most integer division operators round towards zero.

One problem with the shift right operation in high-level languages is that it's rare for a high-level language to support both the logical shift right and the arithmetic shift right. Worse still, the specifications for certain languages leave it up to the compiler's implementer to decide whether to use an arithmetic shift right or a logical shift right operation. Therefore, it's only safe to use the shift right operator on values whose HO bit will cause both forms of the shift right operation to produce the same result. If you need to guarantee that a shift right is a logical shift right or an arithmetic shift right operation, then you'll either have to drop down into assembly language or you'll have to handle the HO bit manually. Obviously, the high-level code gets ugly really fast, so a quick in-line assembly statement might be a better solution if your program doesn't need to be portable across different CPUs. The following code demonstrates how to simulate a 32-bit logical shift right and arithmetic shift right in languages that don't guarantee the type of shift they use:

 // Written in C/C++, assuming 32-bit integers, logical shift right:      // Compute bit 30.      Bit30 = ((ShiftThisValue & 0x800000000) != 0) ? 0x40000000 : 0;      // Shifts bits 0..30.      ShiftThisValue = (ShiftThisValue & 0x7fffffff) >> 1;      // Merge in Bit #30.      ShiftThisValue = ShiftThisValue  Bit30;  // Arithmetic shift right operation      Bits3031 = ((ShiftThisValue & 0x800000000) != 0) ? 0xC0000000 : 0;      // Shifts bits 0..30.      ShiftThisValue = (ShiftThisValue & 0x7fffffff) >> 1;      // Merge bits 30/31.      ShiftThisValue = ShiftThisValue  Bits3031;

Many assembly languages also provide various rotate instructions that recirculate bits through an operand by taking the bits shifted out of one end of the operation and shifting them into the other end of the operand. Few high-level languages provide this operation; fortunately, you won't need it very often. If you do, you can synthesize this operation using the shift operators available in your high-level language:

 // Pascal/Delphi/Kylix Rotate Left, 32-bit example:       // Puts bit 31 into bit 0, clears other bits.       CarryOut := (ValueToRotate shr 31);       ValueToRotate := (ValueToRotate shl 1) or CarryOut;

Assembly language programmers typically have access to a wide variety of shift and rotate instructions. For more information on the type of shift and rotate operations that are possible, consult my assembly language programming book, The Art of Assembly Language (No Starch Press).