Section 3.2. The Pi-Calculus

3.2. The Pi-Calculus

Developed by Scottish mathematician Robin Milner in the 1990s, the pi-calculus is a formal language for defining concurrent, communicating processes, including, but not restricted to, business processes. In its detail, the pi-calculus is a rather advanced algebraic system requiring a senior level of mathematical training. Milner's presentation of the subject is written in the mathematical idiom of definitions, theorems, and lemmas, inaccessible to most BPM onlookers.^[*] Few business analysts or software developers could survive if required to compose their business processes as lines of pi-calculus code.

^[*] R. Milner. "The Polyadic Pi-Calculus: A Tutorial," in F.L. Bauer, W. Brauer, H. Schwichtenberg (editors), Logic and Algebra of Specification," Berlin, Springer, 1993. (Check the "References" section for more Milner works on the subject.)

But somehow, despite its academic roots and its inherent complexity, the pi-calculus has become one of BPM's most attention-getting cocktail party terms. Popular BPM literature states boldly that major languages such as XLANG, WSCI, BPML, BPEL, and WS-CDL are based on the pi-calculus. This stunning level of influence, charges leading BPM commentator Wil van der Aalst, is dubious, and surely nothing but hype:

Let the people that advocate BPEL4WS, BPMN, ... and WSCI show the precise relation between the language and some formal foundation. People that cannot do this but still claim strong relationships between their language and e.g., pi-calculus, only cause confusion.^[*]

^[*] W. M. P. van der Aalst, "Pi calculus versus Petri nets: Let us eat 'humble pie' rather than further inflate the `pi hype,'" http://is.tm.tue.nl/research/patterns/download/pi-hype.pdf.

Whether or not it is hype, the pi-calculus-BPM connection merits a serious look. What, in a nutshell, is the pi-calculus, how does it apply to BPM, and what is the extent and nature of its influence on contemporary popular languages like XLANG and WS-CDL?

NOTE

Robin Milner visited Petri net creator Carl Adam Petri in Bonn in the 1980s to learn more about concurrent systems.

3.2.1. The Pi-Calculus in a Nutshell

As mentioned earlier, the pi-calculus is a language that defines concurrent processes that interact with one another dynamically. Each process consists of one or more actions, which can be arranged sequentially, in parallel or conditional paths, or recursively. An action is the sending or receiving of information on a channel. According the pi-calculus convention, when one process sends information to another, it includes the name of the channel to be used for the other process to respond. This name is variable and, as you will see, can change in response to changing conditions.

The process definition is a set of mathematical equations using defined symbols. Example 3-1 illustrates the interactions of a customer, a travel agent, and an airline in the booking of a travel reservation.

Example 3-1. Travel agency pi-calculus example

 1    Customer(createorder,customer)= 2       
<customer>.customer(result) 3    Agent(createorder,agentok,agentfail,airline)= 4       createorder(customer).
<agentok,agentfail>. 5       Agent1(agentok,agentfail,customer) 6    Agent1(agentok,agentfail,customer)= 7       agentok(result).
<result>+ 8       agentfail(result2).
<result2> 9    Airline(airline,agentok,agentfail)= 10       airline(agentok,agentfail).
<"conf no 121"> 11    End2End= 12       (new corder,cust,ok,fail,air) 13       Customer(corder,cust)|Agent(corder,ok,fail,air)|Airline(air,ok,fail)

The definition of the customer process, which sends an order to a travel agent and waits for a result, appears in lines 1 and 2. Line 1 declares that the process Customer uses channels createorder and customer. In line 2, the process first sends, on channel createorder, bound for the agency, the value customer ( <customer> ), where customer is actually the name of the channel on which it expects a reply. The notation is p<q> means "send q on channel p," and although the content of q is arbitrary, in many cases it is the name of a channel. Next the customer process listens on the channel customer, which originates from the agency, for a result message (customer(result)). The notation p(q) means "receive q on channel p." Separating these two actions is a period (.) representing the sequential operator . In other words, the actions are performed one after another: first the send on channel createorder, then the receive on channel customer.

The process for the travel agent spans lines 3 to 8 and is broken into two parts. The first part, entitled Agent in lines 3 to 5, receives the order request from the customer (createorder(customer)), then sends on the channel airline the values agentok and agentfail ( <agentok,agentfail>), both of which are names of channels on which to receive a response from the airline, and then transitions into the process Agent1. Agent1, in lines 6 through 8, contains two sequences separated by a plus sign (+), representing the conditional operator. Exactly one of these sequences will occur. In the first (line 7), the agent receives a message from the airline on the agentok channel ( agentok(result)), signifying a successful booking, and forwards it to the customer ( <result>); the second case, on line 8, is similar, except that the agent receives a message on the agentfail channel, signifying a failed booking. Combining these definitions, the travel agency receives an order from the customer, sends it to the airline, and waits for a successful or failure event from the airline before forwarding the result to the customer.

The Airline process is defined in lines 9 and 10. (For brevity, the example is kept artificially simplistic.) The airline listens on the channel airline for the names of the channelsagentok, agentfailto be used to respond to the agency, and then sends a confirmation "conf no=121" on the agentok channel.

The process End2End, lines 11 through 13, is the overall concurrent system of Customer, Agent, and Airline. The new statement on line 12, known as the restriction operator, creates private channels to be used among the processes. The pipe symbol in line 13 (|) is the concurrency operator . The processes Customer, Agent, and Airline run simultaneously, interacting over channels localized to the overall process End2End. The overall communication is shown in Figure 3-2.

One of the most distinctive features of the pi-calculus is mobility , in which the topology of communicating processes changes dynamically in response to changing conditions. An example of mobility is the enrollment of customers with retailers in a deregulated energy market. In scenario (1) of Figure 3-3, the customer initially buys energy directly from the supplier (a "standard supply" arrangement). In scenario (2), the customer enrolls with retailer A, and then in scenario (3) switches to competing retailer B. Finally, in scenario (4), the customer decides to drop retailer B, and return to standard supply.

Figure 3-2. Pi-calculus travel agency example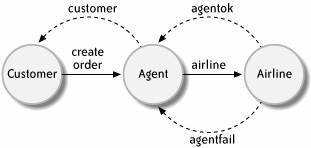

Figure 3-3. Pi-calculus mobility: energy customer switches retailers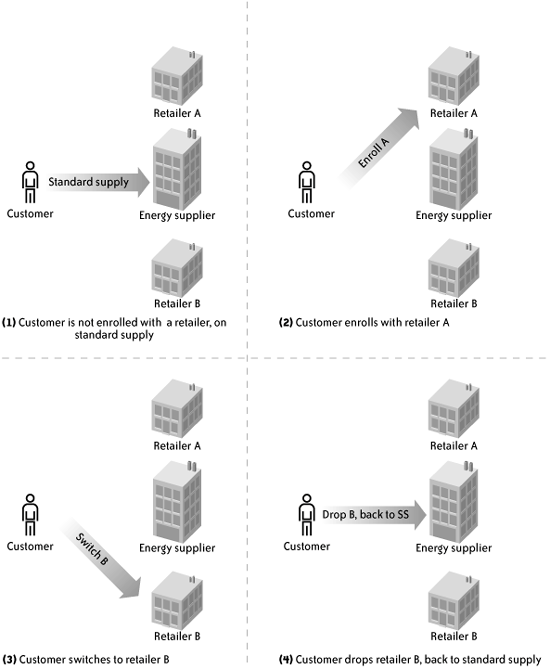

As you can see in Example 3-2, the source code to model this scenario is remarkably terse:

Example 3-2. Energy pi-calculus example

 1    CustomerSS(enroll,switch,drop,rets)= 2       (r:rets).(
<r,mike>.CustomerR(r,enroll,switch,drop,rets)) 3    CustomerR(r,enroll,switch,drop,rets)= 4      (r2:rets).(
<r,r2,mike>.CustomerR(r2,enroll,switch,drop,rets)) + 5       
<r,mike>.CustomerSS(enroll,switch,drop,rets) 6    Supplier(enroll,switch,drop)= 7       (enroll(r1,c).
<"addcust",c> + 8       switch (r1,r2,c).
<"dropcust",c>.
!<"addcust",c> + 9       drop(r1,c).
<"dropcust",c>).Supplier(enroll,switch,drop) 10    Retailer(r)= 11       r(action,c).Retailer(r) 12    Market= 13       (new chEnroll,chSwitch,chDrop,retSet={retA,retB}) 14       CustomerSS(chEnroll,chSwitch,chDrop,retSet)| 15       Supplier(chEnroll,chSwitch,chDrop) | 16       Retailer(retA)|Retailer(retB)

The first two processes in this sample model a customer. The first, CustomerSS in lines 1 and 2, represents a customer on standard supply who enrolls with a retailer. The obscure expression:

      (r: rets).(
<r,"mike">.CustomerR(r,enroll,switch,drop,rets))

means:

• (r:rets): Choose a retailer channel r from the set of retailers rets.

• <r,"mike">: Send r and the customer's name "mike" on the channel enroll.

• CustomerR(r,enroll,switch,drop,rets): Change state to that of an enrolled customer by calling the process CustomerR, passing the chosen value of r.

CustomerR, in lines 3-5, is the process for a customer enrolled with a retailer, who can either switch to a different retailer or drop the current retailer and return to standard supply. The switch option, in line 4:

     (r2 : rets).(
 <r,r2, "mike"> .CustomerR(r2,enroll,switch,drop,rets))

means:

• Choose a retailer channel r2 from the set of retailers rets.

• Send r2, as well as the channel of the retailer with which the customer is currently enrolled, r, and the customer's name "mike" on the channel switch.

• Keep the same state, but change the retailer of record, given by the first variable, from r to r2 by recursively calling the process (CustomerR(r2,enroll,switch,drop,rets)).

The drop option, on line 5, means send r and the customer's name "mike" on the channel drop, then change state to that of a customer on standard supply by calling the process CustomerSS.

The supplier process, in lines 6 to 9, listens on channels enroll, switch, and drop for messages from the customer. In the enrollment case, in line 7, the process receives the message from the customer on the enrollment channel (enroll(r1,c)), and then sends a message to the channel of the specified retailer (r1) to add customer c to its customer base ( <"addcust",c> ). The drop case, in line 9, is similar, but the message from the customer arrives on the channel drop (i.e., drop(r1,c)) and the supplier's message to the retailer is to drop the customer (<"dropcust",c>). The switch case, in line 8 is a combination of drop and enrollment: receive on the switch channel the channels of the new retailer (r2) and old retailer (r1), and then instruct the old retailer to drop the customer and the new retailer to add the customer. When these activities are completed, the supplier process continues recursively (Supplier(enroll,switch,drop)) on line 9), much like a daemon.

The retailer process, in lines 10 and 11, listens on its channel r for the required action and customer (r(action,c)) and then, like the supplier process, continues recursively.

The market process, in lines 12 to 16, creates a simple energy market. Line 13 creates specific instances of the enroll, switch, and drop channels (chEnroll, chSwitch, and chDrop, respectively), as well as a set, named retSet, of actual retailer channels (retA and retB). Lines 14 through16 create four concurrent process instances and pass them to the newly defined channels. The processes include a single customer on standard supply, a supplier, and two retailers using channels retA and retB, respectively. The overall system resembles a web services choreography!

NOTE

The most widely cited example of mobility is the handover protocol used in GSM cell phone networks to switch cell bases for a phone call, as a phone (normally used in a car) moves through two geographic areas.

3.2.2. The Pi-Calculus and BPM

BPM is fast becoming the practical study and design of solutions for elaborate, multiple-company communicating business processes. For those seeking a formal basis for BPM processing, the pi-calculus offers three key features:

Control flow

In the pi-calculus, the sequential, parallel, conditional, and recursive behavior of a process can be declared succinctly.

Message-based communication

The heart of the pi-calculus is its clean syntax and semantics for inbound and outbound messaging.

Mobility

Contemporary processes cannot hardcode service endpoints but requireS the ability to pass around and change addresses dynamically. Dynamic addressing, or mobility, is the most distinctive feature of the pi-calculus.

A good BPM language has the control structures of a flow chart, and has as its most significant steps "mobile" message-based interactions. The major contemporary process languages, as it turns out, are like this anyway. XLANG, for example, has similar control structures (sequence, all, switch), explicit service-oriented message support (the operation action), and dynamic channel bindings. WS-CDL is based on interactions, message exchanges on channels, and channel passing between participants.

NOTE

WS-CDL, according to its author, is based on the Explicit Solos Calculus , a variant of pi-calculus, which allows a system to be modeled from a global viewpoint.^[*] Robin Milner, pi-calculus creator, is an invited expert in the W3C Choreography Working Group .

^[*] N. Kavantzas, "Aggregating Web Services: Choreography and WS-CDL" (presentation), http://www.oracle.com/technology/tech/webservices/htdocs/spec/WS-CDL-April2004.pdf, Oracle, April 2004

The crux of the "hype" criticism of van der Aalst is that the use of the pi-calculus in the creation of contemporary languages is overstated; that perhaps these languages came together more casually and with less academic rigor than advertised. They might resemble the pi-calculus, but they are hardly based on it. His challenge to prove the connection, though stated in polemical language, could inspire a landmark BPM paper.