Chapter 16: The ACECLUS Procedure

Overview

The ACECLUS (Approximate Covariance Estimation for CLUStering) procedure obtains approximate estimates of the pooled within-cluster covariance matrix when the clusters are assumed to be multivariate normal with equal covariance matrices. Neither cluster membership nor the number of clusters need be known. PROC ACECLUS is useful for preprocessing data to be subsequently clustered by the CLUSTER or the FASTCLUS procedure.

Many clustering methods perform well with spherical clusters but poorly with elongated elliptical clusters (Everitt 1980, 77-97). If the elliptical clusters have roughly the same orientation and eccentricity, you can apply a linear transformation to the data to yield a spherical within-cluster covariance matrix, that is, a covariance matrix proportional to the identity. Equivalently, the distance between observations can be measured in the metric of the inverse of the pooled within-cluster covariance matrix. The remedy is difficult to apply, however, because you need to know what the clusters are in order to compute the sample within-cluster covariance matrix. One approach is to estimate iteratively both cluster membership and within-cluster covariance (Wolfe 1970; Hartigan 1975). Another approach is provided by Art, Gnanadesikan, and Kettenring (1982). They have devised an ingenious method for estimating the within-cluster covariance matrix without knowledge of the clusters. The method can be applied before any of the usual clustering techniques, including hierarchical clustering methods.

First, Art, Gnanadesikan, and Kettenring (1982) obtain a decomposition of the total-sample sum-of-squares-and-cross-products (SSCP) matrix into within-cluster and between-cluster SSCP matrices computed from pairwise differences between observations, rather than differences between observations and means. Then, they show how the within-cluster SSCP matrix based on pairwise differences can be approximated without knowing the number or the membership of the clusters. The approximate within-cluster SSCP matrix can be used to compute distances for cluster analysis, or it can be used in a canonical analysis similar to canonical discriminant analysis. For more information, see Chapter 21, 'The CANDISC Procedure.'

Art, Gnanadesikan, and Kettenring demonstrate by Monte Carlo calculations that their method can produce better clusters than the Euclidean metric even when the approximation to the within-cluster SSCP matrix is poor or the within-cluster covariances are moderately heterogeneous. The algorithm used by the ACECLUS procedure differs slightly from the algorithm used by Art, Gnanadesikan, and Kettenring. In the following sections, the PROC ACECLUS algorithm is described first; then, differences between PROC ACECLUS and the method used by Art, Gnanadesikan, and Kettenring are summarized.

Background

It is well known from the literature on nonparametric statistics that variances and, hence, covariances can be computed from pairwise differences instead of deviations from means. (For example, Puri and Sen (1971, pp. 51-52) show that the variance is a U statistic of degree 2.) Let X =( x _ij ) be the data matrix with n observations (rows) and v variables ( columns ), and let x _j be the mean of the j th variable. The sample covariance matrix S =( s _jk ) is usually defined as

The matrix S can also be computed as

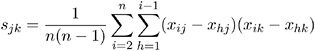
Let W =( w _jk ) be the pooled within-cluster covariance matrix, q be the number of clusters, n _c be the number of observations in the c th cluster, and

The matrix W is normally defined as

where x _cj is the mean of the j th variable in cluster c . Let

The matrix W can also be computed as

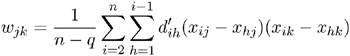
If the clusters are not known, cannot be determined. However, an approximation to W can be obtained by using instead

where u is an appropriately chosen value and M = ( m _jk ) is an appropriate metric. Let A = ( a _jk ) be defined as

If all of the following conditions hold, A equals W :

• all within-cluster distances in the metric M are less than or equal to u

• all between-cluster distances in the metric M are greater than u

• all clusters have the same number of members n _c

If the clusters are of unequal size , A gives more weight to large clusters than W does, but this discrepancy should be of little importance if the population within-cluster covariance matrices are equal. There may be large differences between A and W if the cutoff u does not discriminate between pairs in the same cluster and pairs in different clusters. Lack of discrimination may occur for one of the following reasons:

• The clusters are not well separated.

• The metric M or the cutoff u is not chosen appropriately.

In the former case, little can be done to remedy the problem. The remaining question concerns how to choose M and u . Consider M first. The best choice for M is W ^{ˆ’ 1} , but W is not known. The solution is to use an iterative algorithm:

1. Obtain an initial estimate of A , such as the identity or the total-sample covariance matrix. (See the INITIAL= option in the PROC ACECLUS statement for more information.)

2. Let M equal A ^{ˆ’ 1} .

3. Recompute A using the preceding formula.

4. Repeat steps 2 and 3 until the estimate stabilizes.

Convergence is assessed by comparing values of A on successive iterations. Let A _i be the value of A on the i th iteration and A be the initial estimate of A . Let Z be a user -specified v — v matrix. (See the METRIC= option in the PROC ACECLUS statement for more information.) The convergence measure is

where ... indicates the Euclidean norm, that is, the square root of the sum of the squares of the elements of the matrix. In PROC ACECLUS, Z can be the identity or an inverse factor of S or diag( S ). Iteration stops when e _i falls below a user-specified value. (See the CONVERGE= option or the MAXITER= option in the PROC ACECLUS statement for more information.)

The remaining question of how to choose u has no simple answer. In practice, you must try several different values. PROC ACECLUS provides four different ways of specifying u :

• You can specify a constant value for u . This method is useful if the initial estimate of A is quite good. (See the ABSOLUTE option and the THRESHOLD= option in the PROC ACECLUS statement for more information.)

• You can specify a threshold value t > 0 that is multiplied by the root mean square distance between observations in the current metric on each iteration to give u . Thus, the value of u changes from iteration to iteration. This method is appropriate if the initial estimate of A is poor. (See the THRESHOLD= option in the PROC ACECLUS statement for more information)

• You can specify a value p , 0 < p < 1, to be transformed into a distance u such that approximately a proportion p of the pairwise Mahalanobis distances between observations in a random sample from a multivariate normal distribution will be less than u in repeated sampling. The transformation can be computed only if the number of observations exceeds the number of variables, preferably by at least 10 percent. This method also requires a good initial estimate of A . (See the PROPORTION= option and the ABSOLUTE option in the PROC ACECLUS statement for more information.)

• You can specify a value p , 0 < p < 1, to be transformed into a value t that is then multiplied by 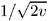times the root mean square distance between observations in the current metric on each iteration to yield u . The value of u changes from iteration to iteration. This method can be used with a poor initial estimate of A . (See the PROPORTION= option in the PROC ACECLUS statement for more information.)

In most cases, the analysis should begin with the last method using values of p between 0.5 and 0.01 and using the full covariance matrix as the initial estimate of A .

Proportions p are transformed to distances t using the formula

where is the quantile (inverse cumulative distribution) function of an F random variable with v and n ˆ’ v degrees of freedom. The squared Mahalanobis distance between a single pair of observations sampled from a multivariate normal distribution is distributed as 2 v times an F random variable with v and n ˆ’ v degrees of freedom. The distances between two pairs of observations are correlated if the pairs have an observation in common. The quantile function is raised to the power given in the preceding formula to compensate approximately for the correlations among distances between pairs of observations that share a member. Monte Carlo studies indicate that the approximation is acceptable if the number of observations exceeds the number of variables by at least 10 percent.

If A becomes singular, step 2 in the iterative algorithm cannot be performed because A cannot be inverted. In this case, let Z be the matrix as defined in discussing the convergence measure, and let Z ² AZ = R ² R where R ² R = RR ² = I and = ( » _jk ) is diagonal. Let be a diagonal matrix where , and 0 < g < 1 is a user-specified singularity criterion (see the SINGULAR= option in the PROC ACECLUS statement for more information). Then M is computed as ZR ² ( *) ^{ˆ’ 1} RZ ² .

The ACECLUS procedure differs from the method used by Art, Gnanadesikan, and Kettenring (1982) in several respects.

• The Art, Gnanadesikan, and Kettenring method uses the identity matrix as the initial estimate, whereas the ACECLUS procedure enables you to specify any symmetric matrix as the initial estimate and defaults to the total-sample covariance matrix. The default initial estimate in PROC ACECLUS is chosen to yield invariance under nonsingular linear transformations of the data but may sometimes obscure clusters that become apparent if the identity matrix is used.

• The Art, Gnanadesikan, and Kettenring method carries out all computations with SSCP matrices, whereas the ACECLUS procedure uses estimated covariance matrices because covariances are easier to interpret than crossproducts.

• The Art, Gnanadesikan, and Kettenring method uses the m pairs with the smallest distances to form the new estimate at each iteration, where m is specified by the user, whereas the ACECLUS procedure uses all pairs closer than a given cutoff value. Kettenring (1984) says that the m - closest -pairs method seems to give the user more direct control. PROC ACECLUS uses a distance cutoff because it yields a slight decrease in computer time and because in some cases, such as widely separated spherical clusters, the results are less sensitive to the choice of distance cutoff than to the choice of m . Much research remains to be done on this issue.

• The Art, Gnanadesikan, and Kettenring method uses a different convergence measure. Let A _i be computed on each iteration using the m -closest-pairs method, and let 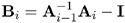where I is the identity matrix. The convergence measure is equivalent to trace .

Analyses of Fisher's (1936) iris data, consisting of measurements of petal and sepal length and width for fifty specimens from each of three iris species, are summarized in Table 16.1. The number of misclassified observations out of 150 is given for four clustering methods:

• k -means as implemented in PROC FASTCLUS with MAXC=3, MAXITER=99, and CONV=0

• Ward's minimum variance method as implemented in PROC CLUSTER

• average linkage on Euclidean distances as implemented in PROC CLUSTER

• the centroid method as implemented in PROC CLUSTER

Table 16.1: Number of Misclassified and Unclassified Observations Using Fisher's (1936) Iris Data

Data	Clustering Method
	k -means	Ward's	Average Linkage	Centroid
raw data	16 [*]	16 [**]	25 + 12 [*]	14 [*]
standardized data	25	26	33+4	33+4
two standardized principal components	29	31	30+9	27+32
four standardized principal components	39	27	32+7	45+11
transformed by ACECLUS P=0.32	39	10+9	7+25
transformed by ACECLUS P=0.16	39	18+9	7+19	7+26
transformed by ACECLUS P=0.08	19	9	3+13	5+16
transformed by ACECLUS P=0.04	4	5	1+19	3+12
transformed by ACECLUS P=0.02	4	3	3	3
transformed by ACECLUS P=0.01	4	4	3	4
transformed by ACECLUS P=0.005	4	4	4	4
canonical variables	3	5	4	4+1
[*] A single number represents misclassi ed observations with no unclassi ed observations. [**] Where two numbers are separated by a plus sign, the rst is the number of misclassied observations; the second is the number of unclassi ed observations.

Each hierarchical analysis is followed by the TREE procedure with NCL=3 to determine cluster assignments at the three-cluster level. Clusters with twenty or fewer observations are discarded by using the DOCK=20 option. The observations in a discarded cluster are considered unclassified.

Each method is applied to

• the raw data

• the data standardized to unit variance by the STANDARD procedure

• two standardized principal components accounting for 95 percent of the standardized variance and having an identity total-sample covariance matrix, computed by the PRINCOMP procedure with the STD option

• four standardized principal components having an identity total-sample covariance matrix, computed by PROC PRINCOMP with the STD option

• the data transformed by PROC ACECLUS using seven different settings of the PROPORTION= (P=) option

• four canonical variables having an identity pooled within-species covariance matrix, computed using the CANDISC procedure

Theoretically, the best results should be obtained by using the canonical variables from PROC CANDISC. PROC ACECLUS yields results comparable to PROC CANDISC for values of the PROPORTION= option ranging from 0.005 to 0.02. At PROPORTION=0.04, average linkage and the centroid method show some deterioration, but k -means and Ward's method continue to produce excellent classifications. At larger values of the PROPORTION= option, all methods perform poorly, although no worse than with four standardized principal components.

This example demonstrates the following:

• PROC ACECLUS can produce results as good as those from the optimal transformation.

• PROC ACECLUS can be useful even when the within-cluster covariance matrices are moderately heterogeneous.

• The choice of the distance cutoff as specified by the PROPORTION= or the THRESHOLD= option is important, and several values should be tried.

• Commonly used transformations such as standardization and principal components can produce poor classifications.

Although experience with the Art, Gnanadesikan, and Kettenring and PROC ACECLUS methods is limited, the results so far suggest that these methods help considerably more often than they hinder the subsequent cluster analysis, especially with normal-mixture techniques such as k -means and Ward's minimum variance method.