MULTIDIMENSIONAL DATABASES

At the abstract level, considering its typical requirements, a multidimensional database (MDDB) is a data repository that provides an integrated environment for decision support queries that require complex aggregations on huge amounts of historical data (e.g., to identify trends in revenues). At the technical level, we assume for this chapter that an MDDB is a relational data warehouse, in which the information is organized following the star-model. Its basic structure may be represented with the simple entity-relationship diagram depicted in Figure 1, in which all the D_i entities represent the dimensions of the MDDB, while the connecting relationship F is the fact table.

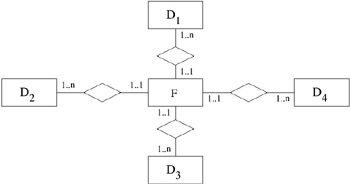
Figure 1: Entity-Relationship Representation of an MDDB

Each dimension table D_i contains all the information that is specific only to the dimension itself (for example, product information), while the fact table F correlates all dimensions and contains information on the attributes of interest for the intersection of all the dimensions (for example, sales by product by day).

Multidimensional queries usually require the computation of aggregate functions on data grouped on an appropriate set of attributes. For multidimensional data processing, data is usually represented as a single (huge) fact table, on which all the interesting aggregates may be computed.

As shown in the practical example below, in addition to the fact table, MDDBs may have several dimensions, each of which is characterized by a considerable number of attributes, most of which may also be relevant for grouping computation.

A Practical Example

We consider as a practical example the MDDB for a large grocery store chain, taken from Kimball (1996). The company manages a large number of stores, each of which is a supermarket selling a wide variety of different products (e.g., grocery, frozen foods, bakery, etc.).

We can identify the following dimensions:

• Product, which can be characterized by more than 50 different attributes describing various features of the products, such as brand, category, diet-type (diet vs. non-diet), package type, weight, case size. Products belong to a merchandise hierarchy, which includes sub-category and category. This means that all the products that belong to the same sub-category also have the same value for attribute category.

• Store, which characterizes each point of sale with attributes such as complete store address and telephone, manager, description of store services, sizes of different departments. Stores are organized in a geographic hierarchy (zip code, county, state). The store dimension may have more than 20 attributes.

• Time, which provides the appropriate detail to allow accurate analysis of the MDDB data, that is indeed a time series. Time is represented with the granularity of day; days may be described as day in the month, in the quarter, and in the year. Furthermore, the indication of which days are holidays, weekend days, days in which special events took place (and many more) can be given. The time dimension may have more than 15 attributes.

• Promotion, which describes the characteristics of product promotions, such as the promotion type (ad, coupon, etc.) and several pieces of information on each promotion type, the promotion cost, and start/end date. Overall the promotion dimension is characterized by at least 10 attributes.

The fact table provides the sales information on which the actual financial analysis is performed. It includes the identifiers of all the dimensions and several attributes describing sales revenues (e.g., income, number of units sold, number of customer transactions performed, etc.). In this chapter we consider a subset of the attributes of each dimension as relevant attributes for grouping computations: we assume 15 attributes for dimensions Product and Store, nine attributes for Time, and 11 attributes for Promotion.

Materialized views in MDDBs

MDDBs have three features that make them an ideal environment for the adoption of materialized views.

• MDDBs are implemented upon data warehouse architectures, where updates occur with a rigid low frequency (daily, weekly, or even monthly), in periods where the system load is low; thus, ratio f_Q / f_U is particularly high.

• MDDBs have a data model that permits the easy adoption of incremental view maintenance techniques; often, materialized views can be maintained considering only the updates and the current state of the materialization, with no need to access base tables.

• Queries in MDDBs can be characterized by a model that permits a precise and manageable definition of the view selection problem.

We now describe the multidimensional data model and the query model. We will then present the most important techniques for the maintenance of materialized views and the MD-mat problem, that is the problem of chosing an optimal set of views to materialize.

Multidimensional Database Model

We repeat for convenience some definitions which were previously introduced.

Definition 1: A Multidimensional Database is a collection of relations D₁, …, D_n, F, where 0

• Each D_i is a dimension table , i.e., a relation characterized by an identifier d_i that uniquely identifies each tuple (d_i is the primary key of D_i).

• F is a fact table , i.e., a relation connecting all dimension tables D₁ , …, D_n ; the identifier of F is given by the foreign keys d₁ , …, d_n of all the dimension tables it connects; the schema of F contains a set of additional attributes V (representing the values on which the aggregate functions are applied).

The dimension tables may contain hierarchies on the data.

Definition 2: Let D be a dimension table with identifier d. An attribute hierarchy on D is a set of functional dependencies FD_D = {fd₀ , fd₁ , …, fd_n }, where each fd_i is characterized by two sets of attributes A ^l_i ⊂ Attr(D) and A^r_i ⊆ Attr(D) (respectively called left side and right side of the dependency); the dependency is represented as fd_i : A ^l_i → A^r_i.

Each functional dependency fd_i is a constraint on the content of the dimension table D: for any pair of tuples t₁, t₂ ∊ D, t₁[A^l_i]= t₂[A^l_i]⇒ t₁[A^r_i]= t₂[A^r_i]. A dependency fd₀ with A ^l₀ = {d} and A ^r₀ = {Attr(D)− d} will always be present in FD_D. A given set of attributes A^l_i may appear only once as the left side of a dependency. Functional dependencies must be acyclic, i.e., the graph obtained by drawing an arc from a_x to a_y, if ∃fd_i ∊ FD_D | a_x ∊ A^l_i ∧ a_y ∊ A^r_i, must be acyclic.

Definition 3: An attribute hierarchy is tree-like (FD ^T ) if all the attributes appear at most once in the right side of a functional dependency and the left side always contains a single attribute.

In this chapter we consider only tree-like attribute hierarchies.

Definition 4: An MDDB attribute hierarchy FD_DB is the union of the attribute hierarchies FD_Dj of all the dimensions D_j appearing in the MDDB.

Business analysis queries usually require the computation of aggregate functions on data grouped on an appropriate set of attributes.

Example 1: Consider again the multidimensional database of our example, MDDB = {Product, Store, Time, Promotion, F}, where each dimension table has its corresponding attributes and with fact table F ={p, s, d, r, f}, having p, s, d (time dimension is represented with the granularity of day), and r as foreign keys of the dimension tables, and f representing the amount of sales. The following queries can be requested on the MDDB:

• q₁ = total sales per product

• q₂ = total sales per product and store

• q₃ = total sales per product and day

• q₄ = total sales per product, store and day

The queries we consider are select-join-group-by queries, with some restrictions on the allowed selection and join predicates. In particular, selection predicates are simple comparison predicates between a dimension attribute and a constant value (i.e., are of the type attr <operator> const-value). These predicates select a "slice" of data on which aggregates are actually computed. We envision a framework where the user provides a set of queries representative of the queries that the system must answer. For select queries we assume that only the attribute used is important and not the constants used in the comparison (which will generally change from query to query). To simplify the framework, we derive from a selection condition on an attribute a request for aggregating on that attribute. Consider a query q that returns the total sales of a particular store grouped by products. Query q can be answered by accessing the result of a query that returns the sales grouped by product and store, and selecting from them only the tuples relative to the specified store. In this way we can focus on queries computing aggregates. These considerations lead to the restriction that all the attributes appearing in a selection predicate must also appear as grouping attributes.

Join operations may be performed only between the fact table and any of its dimensions. Allowed predicates are equality predicates between a dimension identifier and the corresponding fact table foreign key, while join predicates involving non-key attributes are disallowed.

We consider the standard SQL notion of group-by and aggregate function (considered functions are count, sum, avg, min, max). Grouping attributes may be drawn both from dimension and fact table attributes.

Definition 5: Given a query q, we define the query as characterized by the set of its group-by attributes A. We may represent the query as q ^A.

Data-cube

A fundamental characteristic of MDDB queries is that it is often convenient to reuse the results of queries to answer other queries. In Example 1, we can use the result of query q₂ to answer query q₁, adding the sales across all stores to get the result. In a similar way, q₁ can also be computed in terms of the answers to queries q₃ and q₄, while q₂ and q₃ can be computed in terms of query q₄.

The reuse of queries is strictly related to the data-cube (Gray et al., 1996) operator. This operator, receiving as input a table T, a set of aggregating attributes A, and an aggregate function f, computes the union of the results of the queries evaluating function f, having as grouping attributes all possible combinations of attributes in A.

Consider the situation where only the fact table F is present. Applying the data cube operator on the foreign keys of F, we obtain a data cube lattice.

Definition 6: Given an MDDB = {D₁ , …, D_n , F}, the lattice Cube-lattice of MDDB is the lattice of the set of all possible grouping queries that can be defined on the foreign keys of F. This lattice is characterized by the following elements:

• an ordering relation defined as the comparison between the sets of grouping attributes (i.e., q^A1 ≼ ” q^A2 ↔ A₁ ⊆ A₂);

• meet operator as union of the grouping attributes;

• join operator as intersection of the grouping attributes;

• the query grouping on all the foreign keys as top element;

• the query computing the aggregate function on all the tuples of F as bottom element (empty set of grouping attributes).

Requested queries are associated with a subset of the views of the data-cube lattice of MDDB. In Agrawal, Chaudhuri, & Narasayya (2000). the subset of views is considered which appears in the execution plans of representative queries.

Example 2: Consider again the MDDB of Example 1. Figure 2 represents the data-cube lattice derived from the fact table F and shows the elements that have a query associated.

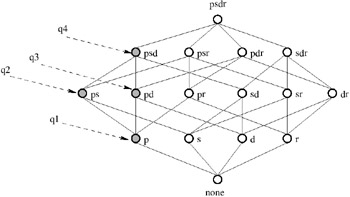
Figure 2: Data-Cube Lattice with Associated Queries

The Multidimensional Lattice

The presence of dimensions significantly increases the size of the problem. The first aspect is the growth in the number of potential grouping attributes, which exponentially increases the number of elements of the lattice. The second aspect is the presence of hierarchies, which permits removal of some elements from the lattice. In fact, consider a query grouping on a dimension key d_i and also on an attribute a_j of the same dimension D_i. Since there exists a functional dependency from d_i to a_j, a query grouping on {d_i , a_j} must produce the same result of the query grouping on {d_i}. This observation is the basis for the following generalization.

Definition 7: Let q_i^Ai and q_j^Aj be two queries and FD_DB the MDDB attribute hierarchy. The operator ancestor (represented by the symbol ⊕) is defined by the following algorithm:

Algorithm 1: Ancestor of two queries.

Algorithm 1 operates by building the union of the attributes characterizing the queries and eliminating all the elements for which there exists a functional dependency in FD_DB.

The result of applying the operator ⊕ to queries q_x and q_y is the smallest view that contains all the information necessary for answering q_x as well as q_y. If applied in a reflexive way (i.e., q_x^Ax ⊕ q_x^Ax), it eliminates all redundant attributes.

Example 3: Consider the Store dimension of the MDDB described earlier, with key s and restricted to a set of attributes {z, c, st, n} representing respectively zip code, county, state, and number of sale clerks. The dimension has the following tree-like attribute hierarchy: { fd₀ : s → {z, c, st, n}, fd₁ : z → c, fd₂ : c → st}.

The queries q ^{n} , q ^{c} , and q ^{st} can for example be computed from q ^{c,n} = q^{n} ⊕ q^{c} ⊕ q ^{st}.

Definition 8: The operator descendent (represented by symbol ⊖ ) is defined by the following algorithm:

Algorithm 2: Descendent of two queries.

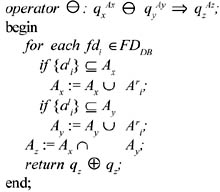
Algorithm 2 first extends the parameters A_x and A_y with all the attributes that can possibly be derived from them. It then considers their intersection A_z and finally removes from it the right sides of dependencies whose left side is contained in A_z.

The descendent operator computes the "greatest" among the set of attributes characterizing the queries that can be computed by both q_x and q_y.

Definition 9: Let {D₁ , …, D_n , F} be a multidimensional database and FD_DB the MDDB attribute hierarchy. Consider the set of queries characterized by all the combinations among the attributes of {D₁ , …, D_n , F}, except the combinations that contain elements on both sides of a functional dependency fd_i ∊ FD_DB . This set of queries identifies a lattice where:

• ⊕ is the meet operation;

• ⊖ is the join operation;

• the ordering relation is given by the following definition: q^A₁ ≼ q^A₂ ↔ (A₁ ⊖ A₂) = A₁ ↔ (A₁ ⊕ A₂) =A₂;

• the query grouping on all the foreign keys of F, {d₁ , …, d_n}, is the top element;

• the query computing the aggregate function on all the tuples of F is the bottom element (empty set of grouping attributes).

We call this lattice the MD-lattice (multidimensional lattice).

Comparing Definitions 6 and 9, it is easy to observe that without hierarchies the MD-lattice is equivalent to the Cube-lattice built on all the schema attributes.

Example 4: Consider the Store dimension of Example 3. The MD-lattice for an MDDB where Store is the only dimension is represented in Figure 3.

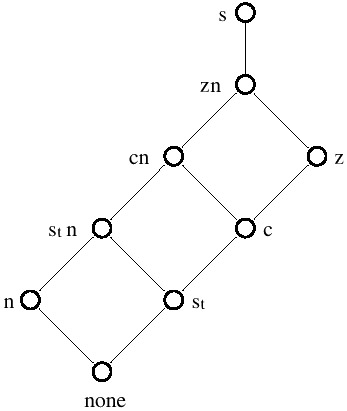
Figure 3: MD-Lattice of the Store Dimension

An MD-lattice defines all possible ways of computing queries that can be defined on an MDDB in terms of other queries defined also on MDDB. In fact, if a query q_i ≼ q_j then q_i can be answered using q_j. This property can be generalized.

Definition 10: Let q_i and q_j be two queries on an MDDB. Then, the least upper bound (l.u.b.) of q_i and q_j in the MD-lattice is the query obtained as a result of evaluating q_i ⊕ q_j , and it represents a query (the most specialized) which can be used to answer both q_i and q_j.

We now distinguish between queries and views. In the following we will use the term query to refer to the representative queries provided by the user, while we will use the term view to refer to the elements of the lattices. When a query q computes the content of a view v of a lattice, we say that the query q is associated with view v. We also extend to views the notation for the queries and say that a view is characterized by a set of attributes A if A is the set of grouping attributes of v, represented as v^A.

Definition 11: A query q_i is said to depend on view v_j if the query can be answered using as only inputs the content of v_j together with any appropriate dimension D_i.

There is a strict relationship between dependence of a query on a view and the ordering relation on an MD-lattice. In fact, if we consider a query q_i depending on view v_j and the view v_i associated with the query, it must happen that v_i≼ v_j.

An important relationship exists between the ordering of the elements in the lattice given by relation ≼ and the cardinalities (i.e., number of tuples) of the views. In fact, for each pair of views v_i , v_j ∊ MD-lattice, if v_j ≺ v_i, v_j can be computed by v_i with a further grouping. Since grouping can only reduce the number of tuples, it follows that |v_j| ≤ |v_i|, where |v| represents the cardinality of v.

Determining the Number of Nodes of an MD-lattice

The number of views of an MD-lattice depends on the number of attributes of the dimensions of the MDDB and on the number and structure of the attribute hierarchies.

In the absence of hierarchies on the dimensional tables, i.e., when each dimension has a hierarchy that contains only the functional dependency between the key of the dimension and all its attributes, the number of views of the MD-lattice is given by the formula:

where i is the number of dimensions of MDDB and n_i is the number of non-key attributes of each dimension D_i. In fact, the number of views of the MD-lattice is obtained as the product of the number of views of the lattices that can be built on every dimension. Each dimension D_i generates a lattice which has 2^n_i elements representing all the possible combinations of n_i attributes (exactly like a Cube-lattice), plus one view which represents the view characterized by the key d_i.

In the presence of hierarchies, the number of views in the local lattices is reduced and the above formula for n_total constitutes an upper bound. A formal treatment of the cardinality of the MD-lattice in the presence of hierarchies is beyond the scope of this chapter. We only provide as an example the determination of the number of elements for the MD-lattice of the MDDB previously described.

Example 5: Consider the MDDB described earlier in this chapter. The number of views of the lattices that can be built on every dimension are: n_Product = 12,289; n_Store = 8,193; n_Time = 129; n_Promotion = 1025. The total number of views of the resulting MD-lattice is then the product of all these values, obtaining | MD-lattice | = 1.3313 · 10¹³.