CHARACTERIZATION OF HIERARCHIES

In this section, we discuss the hierarchies from two different perspectives: the first is the mapping between domain values, i.e., total and partial classification hierarchies, and the second is the hierarchical structure. The latter case introduces multiple hierarchies and multiplicity of hierarchies. Note that the dimension analysis which will be discussed in the rest of this chapter concerns only regular hierarchies; in other words we will consider only hierarchies in which no overlapping exists among the domain instances of each category attribute or variable.

Classification Hierarchies

As we mentioned before, dimensions have often been associated with different hierarchically organized levels. These levels correspond to different granularities of viewing data. The name of each level is expressed by the corresponding variable name. Generally, the shift from a lower (more detailed) level to a higher (more aggregate) level is carried out by a mapping. A mapping between two variables can be complete or incomplete. In the first case the hierarchy is called a total classification hierarchy, and in the second case it is called a partial classification hierarchy. We give the following definitions:

Definition: A mapping between two variables of a hierarchy defines a containment function if each variable instance of a lower level corresponds to only one variable instance of a higher level and each variable instance of a higher level corresponds to at least one variable instance of a lower level. In such a case, this mapping is called full mapping.

Definition: A total classification hierarchy on a given dimension is a hierarchy in which there is a full mapping between each adjacent couple of variables.

The containment function respects the summarizability conditions (disjointness and completeness) of multidimensional databases described in Lenz & Shoshani (1997). As known in the literature, a hierarchy is intentionally represented by a partially ordered set. Therefore, a total classification hierarchy is any subset that defines a total order.

Example 1: Let us consider a nationwide drink company that owns chain stores located in all cities. Let as assume that all stores in the chain sell the same beverages. Sales data are collected yearly, i.e., at the end of each year, each member store reports the total number of sales of each drink to the regional headquarters. Figure 6 shows part of the data reported in 1997 and 1998.

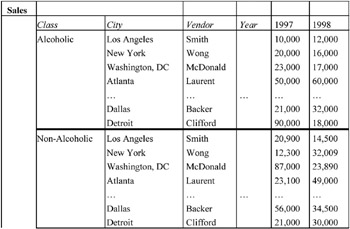
Figure 6: Example of a Data Cube

The hierarchy along the location and beverage dimensions are represented in Figure 7 both in intentional level and extensional level.

Figure 7: The Hierarchy Along Dimensions: Beverages and Location (on the Left) and the Relative Domain Value (on the Right)

As shown in Figure 7, for a domain value of a level on a location dimension, all domain values of the lower level are defined, i.e., it is a classification hierarchy. This is completely in accordance with the hypothesis made in Example 1, where in all cities of the given country such a drink store is located.

Definition: A partial classification hierarchy on a given dimension is a hierarchy in which there is no full mapping between at least one adjacent couple of variables.

Example 2: Let us consider the chain store example we gave in Example 1. Suppose that the chain stores of the above-mentioned company in the state of California are located only in some of its cities (see Figure 8).

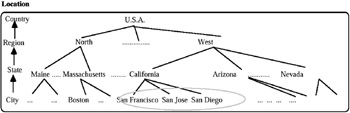
Figure 8: Domain Values of the Level City

Therefore, the domain value of the City level along the Location dimension is restricted compared to that shown in Figure 4. Accordingly, these cities are not listed in the table of Drink Sales.

These two types of hierarchies will influence the result of queries for which the summarization operations will be needed. Details of this fact are discussed in a further section.

Multiplicity of a Hierarchy and Multiple Hierarchies

One of the most important problems regarding hierarchies is their definition. In this section we propose a set of definitions as a reference point for their study.

First of all, we distinguish between the multiplicity of a hierarchy and a multiple hierarchy.

Definition: Let H and H₁ be two hierarchies. H₁ is a multiplicity of H if its level domains are the same as the H level domains, and the variable name associated with each level of H₁ is a specialization of the variable name associated with the corresponding levels of H.

Example 3: Let us consider a location hierarchy defined as: City → Province → Region. A possible multiplicity of this hierarchy is City of residence → Province of residence → Region of residence.

Definition: Let H₁, H₂, …, H_n be a set of hierarchies. This set forms a multiple hierarchy if each of them has at least one variable in common with another hierarchy of the same set.

Example 4: Let us suppose that we have four hierarchies, labeled (a), (b), (c), and (d), as illustrated in Figure 9. The hierarchy labeled (d) is a multiple hierarchy, where the level Province is the same for (a) and (b), and the level Region is the same for (a) and (c).

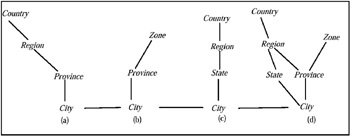
Figure 9: Example of a Multiple Hierarchy

Definition: Let H be a hierarchy. The hierarchy obtained from deleting one or more non-terminal variables or levels of H is a derived hierarchy.

Example 5: From the multiple hierarchy (d) shown in Figure 8, we obtain the following derived hierarchies: City → Province → Country, City → Region → Country, City → Country, City → Zone, City → Region → Country, City → Province → Country, and City → State → Country.

More specifically, in the case of partial classification hierarchies, the variable instances of derived hierarchies are the instances of variables that are adjacent to the instances of deleted levels and between which a connected path can be defined. For example, in Figure 10(b) the variable instances of derived hierarchies obtained from variable instances of the partial classification hierarchy illustrated in Figure 10(a) that satisfy the above mentioned condition are reported.

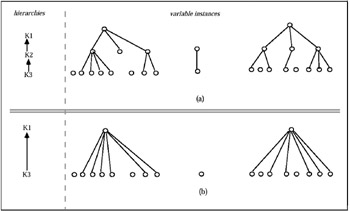
Figure 10: Example of Path Generation Between Levels