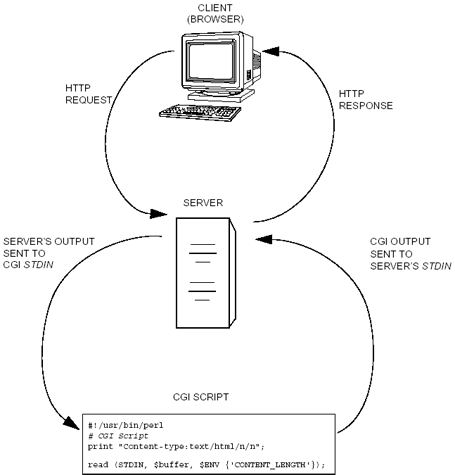
C.4 How HTML and CGI Work Together | JavaScript by Example (2nd Edition)

As previously discussed, HTML is the markup language used to determine the way a Web page will be displayed. CGI is a protocol that allows the server to extend its functionality. A CGI program is executed on behalf of the server mainly to process forms such as a registration form or a shopping list. If you have purchased a book or CD from Amazon.com, you know what a form looks like. When a browser (client) makes a request of the server, the server examines the URL. If the server sees cgi-bin as a directory in the path , it will go to that directory, open a pipe, and execute the CGI program. The CGI program gets its input from the pipe and sends its standard output back though the pipe to the server. Standard error is sent to the server's error log . If the CGI program is to talk to the server, it must speak the Web language, since this is the language that is ultimately used by the browser to display a page. The CGI program then will format its data with HTML tags and send it back to the HTTP server. The server will then return this document to the browser where the HTML tags will be rendered and displayed to the user .

Figure C.3. The client/server/CGI program relationship.

graphics/ap03fig03.gif

C.4.1 A Simple CGI Script

The following Perl script consists of a series of print statements, most of which send HTML output back to STDOUT (piped to the server). This program is executed directly from the CGI directory, cgi-bin . Some servers require that CGI script names end in . cgi or .pl so that they can be recognized as CGI scripts. After creating the script, the execute permission for the file must be turned on. For UNIX systems, at the shell prompt type

 chmod 755 <scriptname>

 chmod +x <scriptname>

The URL entered in the browser Location window includes the protocol, the name of the host machine, the directory where the CGI scripts are stored, and the name of the CGI script. The URL will look like this:

http:// servername /cgi-bin/perl_script.pl

The HTTP Headers

The first line of output for most CGI programs is an HTTP header that tells the browser what type of output the program is sending to it. Right after the header line, there must be a blank line and two newlines. The two most common types of headers, also called MIME types (which stands for multipurpose Internet extension), are "Content-type: text/html\n\n" and "Content-type: text/plain\n\n." Another type of header is called the Location header, which is used to redirect the browser to a different Web page. And finally, Cookie headers are used to set cookies for maintaining state; that is, keeping track of information that would normally be lost once the transaction between the server and browser is closed.

Table C.5. HTTP headers.

Header	Type	Value
Content-type:	text/plain	Plain text
Content-type:	text/html	HTML tags and text
Content-type:	image/gif	GIF graphics
Location:	http://www....	Redirection to another Web page
Set-cookie : NAME=VALUE...	Cookie	Set a cookie on a client browser

Right after the header line, there must be a blank line. This is accomplished by ending the line with \n\n in Perl.

Example C.6

 1  #!/bin/perl  2  print "Content-type: text/html\n\n  ";    #  The HTTP header  3   print "<HTML><HEAD><TITLE> CGI/Perl First Try</TITLE></HEAD>\n"; 4   print "<BODY BGCOLOR=Black TEXT=White>\n"; 5   print "<H1><CENTER> Howdy, World! </CENTER></H1>\n"; 6   print "<H2><CENTER> It's "; 7   print "<!--comments -->";  # This is how HTML comments are   included  8  print `date`;   # Execute the UNIX date command  9   print "and all's well.\n"; 10  print "</H2></BODY></HTML>\n";

EXPLANATION

This first line is critical. Many Web servers will not run a CGI script if this line is missing. This tells the server where Perl is installed.
This line is called the MIME header . No matter what programming language you are using, the first output of your CGI program must be a MIME header followed by two newlines. This line indicates what type of data your application will be sending. In this case, the CGI script will be sending HTML text back to the server. The \n\n cause a blank line to be printed. The blank line is also crucial to success of your CGI program.
The next lines sent from Perl back to the server are straight HTML tags and text. This line creates the header information, in this case, a title for the document.
This defines the background color as black and the textual material as white.
<H1> is a level 1 heading. It is the largest of the headings and prints in bold text. Howdy, World! will be formatted as a level 1 heading and centered on the page.
All text from this point until line 10 will be formatted as a level 2, centered heading.
This is how comments are inserted into an HTML document. They are not displayed by the browser.
The UNIX date command is executed and its output is included as part of the centered, second-level heading. A better way to get the date so that your program is portable is to use localtime , a Perl built-in. Try changing line 9 to

$now = localtime;

print "$now\n" ;)
This line is printed as part of heading level 2.
These tags end the second level heading, the body of the document and the HTML document itself.

Figure C.4. Output from the CGI program in Example C.6.

graphics/ap03fig04.jpg