26.2 Definitions

---

26.2 Definitions

Formally, F_<: is obtained by combining the types and terms of System F from Chapter 23 with the subtype relation from Chapter 15 and refining universal quantifiers to carry subtyping constraints. Bounded existential quantifiers can be defined similarly, as we shall see in §26.5.

There are actually two reasonable ways of defining the subtyping relation of F_<:, differing in their formulation of the rule for comparing bounded quantifiers (S-All): a more tractable but less flexible version called the kernel rule, and a more expressive but technically somewhat problematic full subtyping rule. We discuss both versions in detail in the following subsections, introducing the kernel variant in the first several subsections and then the full variant in §26-1. When we need to be precise about which variant we are talking about, we call the versions of the whole system with these rules kernel F_<: and full F_<:, respectively. The unqualified name F_<: refers to both systems.

Figure 26-1 presents the full definition of kernel F_<:, with differences from previous systems highlighted.

Bounded and Unbounded Quantification

One point that is immediately obvious from this figure is that the syntax of F_<: provides only bounded quantification: the ordinary, unbounded quantification of pure System F has disappeared. The reason for this is that we do not need it: a bounded quantifier whose bound is Top ranges over all subtypes of Top—that is, over all types. So we recover unbounded quantification as an abbreviation:

We use this abbreviation frequently below.

Scoping

An important technical detail that is not obvious in Figure 26-1 concerns the scoping of type variables. Obviously, whenever we talk about a typing statement of the form Г ⊢ t : T, we intend that the free type variables in t and T should be in the domain of Г. But what about free type variables appearing in the types inside Г? In particular, which of the following contexts should be considered to be well-scoped?

•  

  Г1	=	X<:Top, y:X→Nat
  Г2	=	y:X→Nat, X<:Top
  Г3	=	X<:{a:Nat,b:X}
  Г4	=	X<:{a:Nat,b:Y}, Y<:{c:Bool,d:X}

Г₁ is certainly well-scoped: it introduces a type variable X and then a term variable y whose type involves X. A term that might give rise to this context during typechecking would have the form X<:Top. λy:X→Nat. t, and it is clear that the X in the type of y is bound by the enclosing λ. On the other hand, by the same reasoning Г₂ looks wrong, since in the sort of term that would give rise to it—e.g., λy:X→Nat. λX<:Top. t—is it not clear what the intended scope of X is.

Г₃ is a more interesting case. We could argue that it is clear, in a term like λX<:{a:Nat,b:X}. t, where the second X is bound. All we need to do is to regard the scope of the binding for X as including its own upper bound (and everything to the right of the binding, as usual). The variety of bounded quantification incorporating this refinement is called F-bounded quantification (Canning, Cook, Hill, Olthoff, and Mitchell, 1989b). F-bounded quantification often appears in discussions of types for object-oriented programming, and has been used in the GJ language design (Bracha, Odersky, Stoutamire, and Wadler, 1998). However, its theory is somewhat more complex than that of ordinary F_<: (Ghelli, 1997; Baldan, Ghelli, and Raffaetà, 1999), and it only becomes really interesting when recursive types are also included in the system (no non-recursive type X could satisfy a constraint like X<:{a:Nat,b:X}).

Yet more general contexts like Г₄, permitting mutual recursion between type variables via their upper bounds, are not unheard of. In such calculi, each new variable binding is generally allowed to introduce an arbitrary set of inequations involving the new variable and all the existing ones.

We will not consider F-bounded quantification further in this book, and will take all of Г₂, Г₃, and Г₄ to be ill-scoped. More formally, we will require that, whenever we mention a type T in a context, the free variables of T should be bound in the portion of the context to the left of where T appears.

Subtyping

Type variables in F_<: have associated bounds (just as ordinary term variables have associated types), and we must keep track of these bounds during both subtyping and typechecking. We do this by changing the type bindings in contexts to include an upper bound for each type variable. These bounds are used during subtyping to justify steps of the form "the type variable X is a subtype of the type T because we assumed it was."

Adding this rule implies that subtyping now becomes a three-place relation—that is, every subtyping statement will now have the form Г ⊢ S <: T, pronounced "S is a subtype of T under assumptions Г." We complete this refinement by adding contexts to all the other subtyping rules (see Figure 26-1).

Besides the new rule for variables, we must also add a subtyping rule for comparing quantified types (S-All). Figure 26-1 gives the simpler variant, called the kernel rule, in which the bounds of the two quantifiers being compared must be identical.

The term "kernel" comes from Cardelli and Wegner's original paper (1985), where this variant of F_<: was called Kernel Fun.

26.2.1 Exercise [⋆ ↛]

Draw a subtyping derivation tree showing that B→Y <: X→B under the context Г = B<:Top, X<:B, Y<:X.

Typing

We must also refine the typing rules for ordinary universal types. These extensions are straightforward: in the introduction rule for bounded quantifiers, we carry the bound from the abstraction into the context during the typechecking of the body,

and in the elimination rule we check that the supplied type argument actually satisfies the bound:

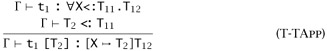
Full F_<:

In kernel F_<:, two quantified types can be compared only if their upper bounds are identical. If we think of a quantifier as a sort of arrow type (whose elements are functions from types to terms), then the kernel rule corresponds to a "covariant" restriction of the standard subtyping rule for arrows, in which the domain of an arrow type is not allowed to vary in subtypes:

This restriction looks rather unnatural, both for arrows and for quantifiers. This analogy suggests that we should refine the kernel S-ALL rule to allow contravariant subtyping in the "left-hand side" of bounded quantifiers, as shown in Figure 26-2.

Figure 26-2: "Full" Bounded Quantification

Intuitively, the full version of S-ALL can be understood as follows. A type T = "X<:T₁.T₂ describes a collection of functions from types to values, each mapping subtypes of T₁ to instances of T₂. If T₁ is a subtype of S₁, then the domain of T is smaller than that of S = "X<:S₁ .S₂, so S is a stronger constraint and describes a smaller collection of polymorphic values. Moreover, if, for each type U that is an acceptable argument to the functions in both collections (i.e., one that satisfies the more stringent requirement U <: T₁), the U-instance of S₂ is a subtype of the U-instance of T₂, then S is a "pointwise stronger" constraint and again describes a smaller collection of values.

The system with just the kernel subtyping rule for quantified types is called Kernel F_<:. The same system with the full quantifier subtyping rule is called Full F_<:. The bare name F_<: refers ambiguously to both systems.

26.2.2 Exercise [⋆ ↛]

Give a couple of examples of pairs of types that are related by the subtype relation of full F_<: but are not subtypes in kernel F_<:.

26.2.3 Exercise [⋆⋆⋆⋆]

Can you find any useful examples with this property?

---