Log-Concavity Conditions

---

To use the ARS sampling method in our Gibbs sampler scheme, we need to show that

and where p denotes the joint posterior distribution.

Now if we let , then equation (17) becomes (up to proportionality)

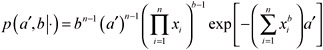
So

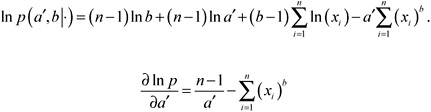
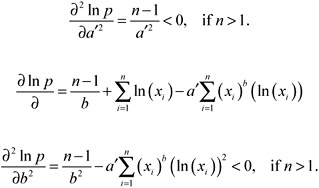
Since and , the conditional marginal posterior densities of parameters a' and b are log-concave. Thus we can employ the ARS method in our Gibbs sampler scheme.

To perform Gibbs sampling, we run the chain for 20,000 times and discard the first 1,000 values as "burn-in." The "burn-in" is needed because of the fact that chains are initialized with values not actually drawn from the posterior distribution, and the simulated values of θ obtained at the beginning of a MCMC run are not distributed from the posterior distribution. However, after some number of iterations have been performed (the burn-in period), the effect of the initial values wears off and the distribution of the new iterates approach the true posterior distribution.

Posterior Predictive Distribution

A major aspect of the Bayesian paradigm is prediction. The posterior predictive distribution of a future observation vector z given the data D is defined as

(18) 

where f(z | θ) denotes the sampling density of z, and π(θ | D) is the posterior distribution of θ. We see that (18) is just the posterior expectation of f(z | θ), and thus sampling from (18) is easily accomplished via the Gibbs sampler from π(θ | D). This is a nice feature of the Bayesian paradigm since (18) shows that the predictions and predictive distributions are easily computed once samples from π(θ| D) are available. After we obtain the posterior predictive distribution, we can use the classical formula (Kendall, Stuart, & Ord, 1977)

(19) 

to find the estimate of the mode. Of course, one can use other methods such as linear interpolation to approximate the mode of the empirical distribution. However given a very large sample size value such as the sample size that we used in the following simulation studies (n = 20,000), Eq. (19) is considered to be quite adequate to locate the mode.

---