Recipe 6.16. Working with Complex Numbers
ProblemYou want an easy way to calculate with complex numbers. SolutionSample code folder: Chapter 06\ComplexNumbers Create a ComplexNumber structure. Overload the standard mathematical operators so that using complex number variables is easy and natural. DiscussionThis recipe provides a great way to see how overloading standard operators can enhance the usability of your classes and structures. In this case, we've created a ComplexNumber structure. Structures are similar to classes, except that they exist as value types rather than reference types. This allows complex number instances to act the same as other simple variables, such as standard numerical variables. The following code defines the ComplexNumber number structure. Place this code in its own file named ComplexNumber.vb for easy inclusion in any application that requires complex numbers: Structure ComplexNumber Public Real As Double Public Imaginary As Double Public Sub New(ByVal realPart As Double, _ ByVal imaginaryPart As Double) Me.Real = realPart Me.Imaginary = imaginaryPart End Sub Public Sub New(ByVal sourceNumber As ComplexNumber) Me.Real = sourceNumber.Real Me.Imaginary = sourceNumber.Imaginary End Sub Public Overrides Function ToString() As String Return Real & "+" & Imaginary & "i" End Function Public Shared Operator +(ByVal a As ComplexNumber, _ ByVal b As ComplexNumber) As ComplexNumber ' ----- Add two complex numbers together. Return New ComplexNumber(a.Real + b.Real, _ a.Imaginary + b.Imaginary) End Operator Public Shared Operator -(ByVal a As ComplexNumber, _ ByVal b As ComplexNumber) As ComplexNumber ' ----- Subtract one complex number from another. Return New ComplexNumber(a.Real - b.Real, _ a.Imaginary - b.Imaginary) End Operator Public Shared Operator *(ByVal a As ComplexNumber, _ ByVal b As ComplexNumber) As ComplexNumber ' ----- Multiply two complex numbers together. Return New ComplexNumber(a.Real * b.Real - _ a.Imaginary * b.Imaginary, _ a.Real * b.Imaginary + a.Imaginary * b.Real) End Operator Public Shared Operator /(ByVal a As ComplexNumber, _ ByVal b As ComplexNumber) As ComplexNumber ' ----- Divide one complex number by another. Return a * Reciprocal(b) End Operator Public Shared Function Reciprocal( _ ByVal a As ComplexNumber) As ComplexNumber ' ----- Calculate the reciprocal of a complex number; ' that is, the 1/x calculation. Dim divisor As Double ' ----- Check for divide-by-zero possibility. divisor = a.Real * a.Real + a.Imaginary * a.Imaginary If (divisor = 0.0#) Then Throw New DivideByZeroException ' ----- Perform the operation. Return New ComplexNumber(a.Real / divisor, _ -a.Imaginary / divisor) End Function End Structure The overloaded New() function lets you instantiate a ComplexNumber number using either a pair of numbers (the real and imaginary parts) or another ComplexNumber number. The following code demonstrates how complex numbers are created and how standard operators allow mathematical operations such as addition and subtraction in a natural way. The overloaded + operator also impacts the += assignment operator. The last example in the code demonstrates this by adding complex number b to complex number a using the new assignment-operator syntax: Dim result As New System.Text.StringBuilder Dim a As ComplexNumber Dim b As ComplexNumber Dim c As ComplexNumber a = New ComplexNumber(3, 4) b = New ComplexNumber(5, -2) c = a + b result.AppendLine(" Complex Numbers") result.AppendLine("a = " & a.ToString()) result.AppendLine("b = " & b.ToString()) ' ----- Addition. c = a + b result.AppendLine("a + b = " & c.ToString()) ' ----- Subtraction. c = a - b result.AppendLine("a - b = " & c.ToString()) ' ----- Multiplication. c = a * b result.AppendLine("a * b = " & c.ToString()) ' ----- Division. c = a / b result.AppendLine("a / b = " & c.ToString()) ' ----- Addition as assignment. a += b result.AppendLine("a += b … a = " & a.ToString()) MsgBox(result.ToString()) The ToString() function is overridden in the ComplexNumber structure to format the real and imaginary parts. Figure 6-16 shows the output from the sample code. Figure 6-16. Working with complex numbers in VB 2005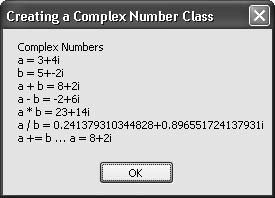 See AlsoSearch for " complex numbers" on the Web for more information on this subject. |
EAN: 2147483647
Pages: 400