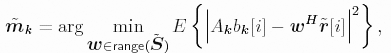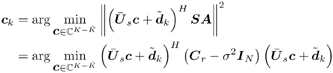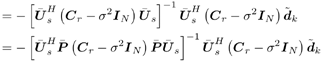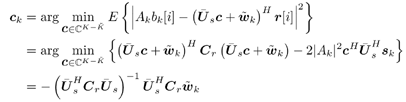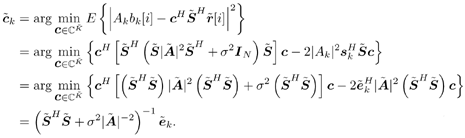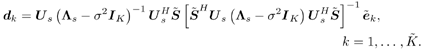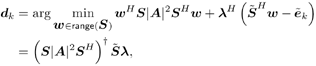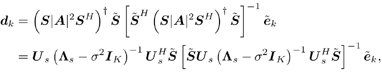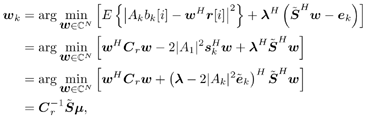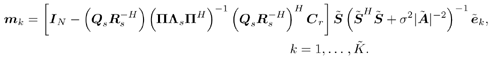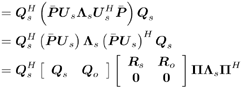3.2 Linear Group-Blind Multiuser Detection for Synchronous CDMA
3.2 Linear Group -Blind Multiuser Detection for Synchronous CDMAWe start by considering the following discrete-time signal model for a synchronous CDMA system: Equation 3.1 Equation 3.2 where, as before, K is the total number of users; A k , b k [ i ], and s k are, respectively, the complex amplitude, i th transmitted bit, and signature waveform of the k th user ; n [ i ] ~ N c (0, s 2 I N ) is a complex Gaussian noise vector; It is assumed that the users' signature waveforms are linearly independent (i.e., S has full column rank). Hence both Equation 3.3 The problem of linear group-blind multiuser detection can be stated as follows . Given prior knowledge of the signature waveforms Equation 3.4 and Equation 3.5 or Equation 3.6 The basic idea behind the solution to the problem above is to suppress the interference from known users based on the signature waveforms of these users and to suppress the interference from other unknown users using subspace-based blind methods . We first consider the linear decorrelating detector, which eliminates the multiple-access interference (MAI) completely, at the expense of enhancing the noise level. To facilitate the derivation of its group-blind form, we need the following alternative definition of this detector. In this section we denote Definition 3.1: [Group-blind linear decorrelating detector ”synchronous CDMA] The weight vector d k of the linear decorrelating detector for user k is given by the solution to the following constrained optimization problem: Equation 3.7 This definition is equivalent to the one given in Section 2.2.2. To see this, it suffices to show that Equation 3.8 Under the constraint The second linear group-blind detector considered here is a hybrid detector that zero-forces the interference caused by the Definition 3.2: [Group-blind linear hybrid detector ”synchronous CDMA] The weight vector w k of the group-blind linear hybrid detector for user k is given by the solution to the following constrained optimization problem: Equation 3.9 Another form of linear group-blind detector is analogous to the linear MMSE detector introduced in Section 2.2.3. It suppresses the interference from the known users and that from the unknown users separately, both in the MMSE sense. First define the following projection matrix: Equation 3.10 which projects any signal onto the subspace null ( Equation 3.11 where Equation 3.12 where Definition 3.3: [Group-blind linear MMSE detector ”synchronous CDMA] Let Equation 3.13 Equation 3.14 Note that in general the linear group-blind MMSE detector m k defined above is different from the linear MMSE detector defined in Section 2.2.3, due to the specific structure that the former imposes. We next give expressions for the three linear group-blind detectors defined above in terms of the known users' signature waveforms Proposition 3.1: [Group-blind linear decorrelating detector (form I) ”synchronous CDMA] The weight vector of the group-blind linear decorrelating detector for user k is given by Equation 3.15 Proof: Decompose d k as Equation 3.16 Hence d k has the form Equation 3.17 Equation 3.18 Equation 3.19 Equation 3.20 where (3.17) follows from (3.11); (3.18) follows from the fact that Equation 3.21 Proposition 3.2: [Group-blind linear hybrid detector (form I) ”synchronous CDMA] The weight vector of the group-blind linear hybrid detector for user k is given by Equation 3.22 Proof: Decompose w k as Equation 3.23 Hence Equation 3.24 Equation 3.25 where (3.24) follows from the fact that Equation 3.26 Proposition 3.3: [Group-blind linear MMSE detector (formI) ”synchronous CDMA] The weight vector of the group-blind linear MMSE detector for user k is given by Equation 3.27 Proof: We first solve for Equation 3.28 Next we solve Equation 3.29 Therefore, we have Equation 3.30 Based on the results above, we can implement the linear group-blind multiuser detection algorithms based on the received signals Algorithm 3.1: [Group-blind linear hybrid detector (form I) ”synchronous CDMA]
Equation 3.34 Equation 3.35 The group-blind linear decorrelating detector and the group-blind linear MMSE detector can be implemented similarly. Note that both of them require an estimate of the noise variance s 2 . A simple estimator of s 2 is the average of the N “ K eigenvalues in Equation 3.36 Hence In the results above, the linear group-blind detectors are expressed in terms of the known users' signature waveforms Equation 3.37 The linear group-blind detectors can also be expressed in terms of the signal subspace components L s and U s of all users' signals defined in (3.37), as given by the following three results. Proposition 3.4: [Group-blind linear decorrelating detector (form II) ”synchronous CDMA] The weight vector of the group-blind linear decorrelating detector for user k is given by Equation 3.38 Proof: Using the method of Lagrange multipliers to solve the constrained optimization problem (3.7), we obtain Equation 3.39 where Equation 3.40 Hence Equation 3.41 where (3.41) follows from (3.11), (3.37), and the fact that Proposition 3.5: [Group-blind linear hybrid detector (form II) ”synchronous CDMA] The weight vector of the group-blind linear hybrid detector for user k is given by Equation 3.42 Proof: Using the method of Lagrange multipliers to solve the relaxed optimization problem (3.9) over Equation 3.43 where Equation 3.44 Hence Equation 3.45 where (3.45) follows from (3.11), (3.37), and the fact that To form the group-blind linear MMSE detector in terms of the signal subspace U s , we first need to find a basis for the subspace range ( Equation 3.46 where Q s is an N x Proposition 3.6: [Group-blind linear MMSE detector (form II) ”synchronous CDMA] The weight vector of the group-blind linear MMSE detector for user k is given by Equation 3.47 Proof: Since the columns of Q s form an orthogonal basis of range ( Equation 3.48 Furthermore, we have Equation 3.49 Equation 3.50 Equation 3.51 Equation 3.52 where (3.49) follows from Based on the results above, we can implement the form II linear group-blind multiuser detection algorithms based on the received signals Algorithm 3.2: [Group-blind linear hybrid detector (form II) ”synchronous CDMA]
In summary, for both the group-blind zero-forcing detector and the group-blind hybrid detector, the interfering signals from known users are nulled out by a projection of the received signal onto the orthogonal subspace of these users' signal subspace. The unknown interfering users' signals are then suppressed by identifying the subspace spanned by these users, followed by a linear transformation in this subspace based on the zero-forcing or MMSE criterion. In the group-blind MMSE detector, the interfering users from the known and unknown users are suppressed separately under the MMSE criterion. The suppression of the unknown users again relies on identification of the signal subspace spanned by these users. |
EAN: 2147483647
Pages: 91
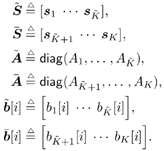
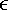
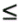
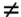
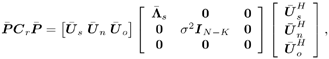
 null (
null (