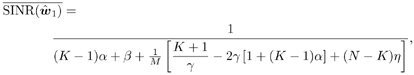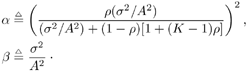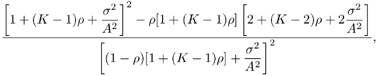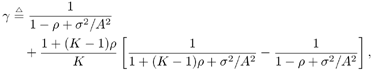2.5 Performance of Blind Multiuser Detectors
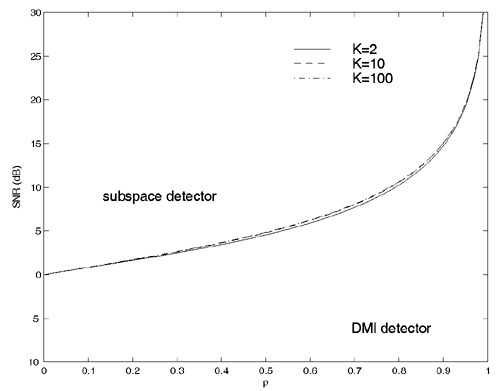
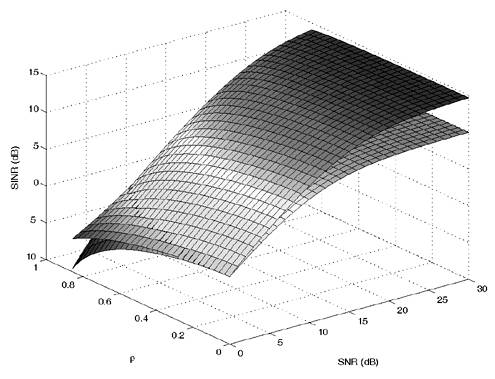
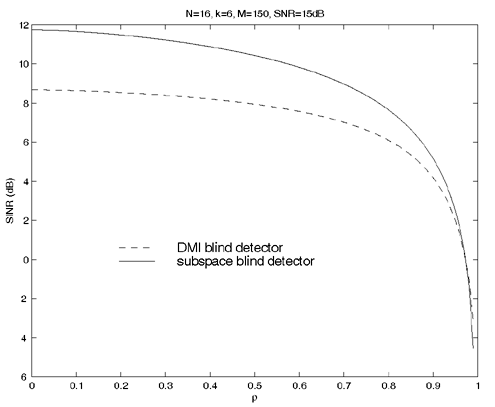
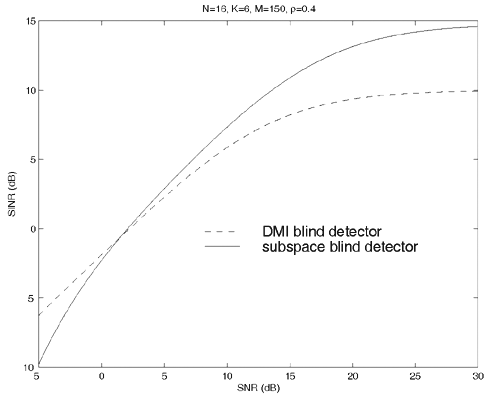
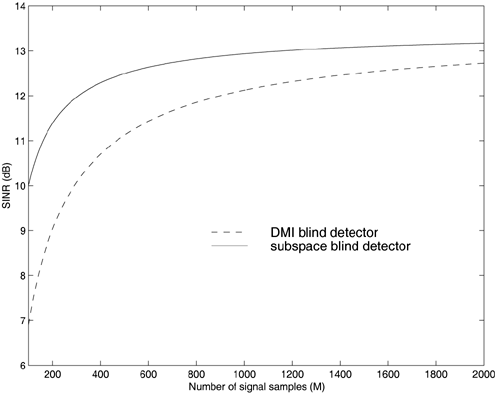
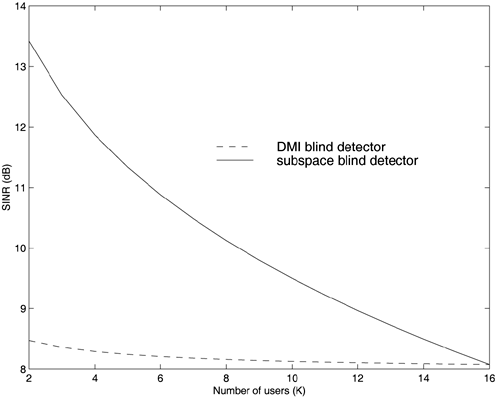
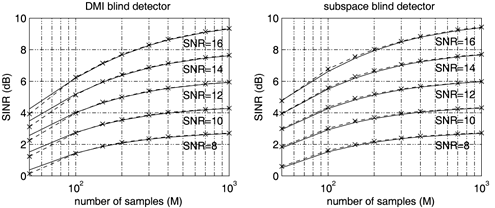
2.5.1 Performance MeasuresIn previous sections we have discussed two approaches to blind multiuser detection: the direct method and the subspace method. These two approaches are based primarily on two equivalent expressions for the linear MMSE detector [i.e., (2.26) and (2.78)]. When the autocorrelation C r of the received signals is known exactly, the two approaches have the same performance. However, when C r is replaced by the corresponding sample autocorrelation, quite interestingly, the performance of these two methods is very different. This is due to the fact that these two approaches exhibit different estimation errors on the estimated detector [193, 194, 197]. In this section we present a performance analysis of the two blind multiuser detectors: the DMI blind detector and the subspace blind detector. For simplicity, we consider only real-valued signals [i.e., in (2.4), A k > 0, k =1, ..., K and n [ i ]~ N ( , s 2 I N )]. Suppose that a linear weight vector Equation 2.115 The bit-error probability of the linear detector using weight vector w 1 is given by Equation 2.116 Now suppose that an estimate Equation 2.117 Obviously, both Equation 2.118 where the first term in (2.118) represents the output of the true weight vector w 1 , which has the same form as (2.10). The second term in (2.118) represents an additional noise term caused by the estimation error D w 1 . Hence from (2.118) the average SINR at the output of any unbiased estimated linear detector Equation 2.119 with Equation 2.120 where If we assume further that D w 1 is actually independent of r [ i ], the average bit-error rate (BER) of this detector is given by Equation 2.121 where From the discussion above it is seen that to obtain the average SINR at the output of the estimated linear detector 2.5.2 Asymptotic Output SINRWe first present the asymptotic distribution of the two forms of blind linear MMSE detectors for a large number of signal samples, M . Recall that in the direct-matrix-inversion (DMI) method, the blind multiuser detector is estimated according to Equation 2.122 Equation 2.123 In the subspace method, the estimate of the blind detector is given by Equation 2.124 Equation 2.125 where Theorem 2.1: Let w 1 be the true weight vector of the linear MMSE detector given by Equation 2.126 and let Equation 2.127 Then with Equation 2.128 where Equation 2.129 Equation 2.130 Hence for large M , the covariance of the blind linear detector, Equation 2.131 The next result gives an expression for the average output SINR, defined by (2.119), of the blind linear detectors. The proof is given in the Appendix (Section 2.8.3). Corollary 2.1: The average output SINR of the estimated blind linear detector is given by Equation 2.132 where Equation 2.133 Equation 2.134 Equation 2.135 It is seen from (2.132) that the performance difference between the DMI blind detector and the subspace blind detector is caused by the single parameter t given by (2.130) ”the detector with a smaller t has a higher output SINR. Let m 1 , ..., m K be the eigenvalues of the matrix R given by (2.131). Denote m min = min 1 Corollary 2.2: If Proof: By rewriting (2.130) as Equation 2.136 we obtain the following sufficient condition under which t subspace < t DMI : Equation 2.137 On the other hand, note that Equation 2.138 Since the nonzero eigenvalues of SS T are the same of those of R = S T S , it follows from (2.138) that Equation 2.139 The first part of the corollary then follows by combining (2.137) and (2.139). The second part of the corollary follows a similar proof. The next result gives an upper and a lower bound on the parameter t in terms of the desired user's amplitude A 1 , the noise variance s 2 , and the two extreme eigenvalues of C r . Corollary 2.3: The parameter t defined in (2.130) satisfies Proof: The proof follows from (2.136) and the following fact from Chapter 4 [cf. Proposition 4.2]: Equation 2.140 To gain some insight from the result (2.132), we next consider two special cases for which we compare the average output SINRs of the two blind detectors. Example 1: Orthogonal Signals In this case, we have u k = s k , R = I K , and Equation 2.141 Substituting (2.141) into (2.132), and using the fact that in this case Equation 2.142 where Example 2: Equicorrelated Signals with Perfect Power Control In this case it is assumed that Equation 2.143 with Equation 2.144 Equation 2.145 Equation 2.146 and Equation 2.147 A necessary and sufficient condition for the subspace blind detector to outperform the DMI blind detector is Equation 2.148 where Figure 2.2. Partition of the SNR “ r plane according to the relative performance of two blind detectors. For each K , in the region above the boundary curve, the subspace blind detector performs better, whereas in the region below the boundary curve, the DMI blind detector performs better. The average output SINR as a function of SNR and r for both blind detectors is shown in Fig. 2.3 It is seen that the performance of the subspace blind detector deteriorates in the high-cross-correlation and low-SNR region; the performance of the DMI blind detector is less sensitive to cross-correlation and SNR in this region. This phenomenon is shown more clearly in Figs. 2.4 and 2.5, where the performance of the two blind detectors is compared as a function of r and SNR, respectively. The performance of the two blind detectors as a function of the number of signal samples M is plotted in Fig. 2.6, where it is seen that for large M , both detectors converge to the true linear MMSE detector, with the subspace blind detector converging much faster than the DMI blind detector; and the performance gain offered by the subspace detector is quite significant for small values of M . Finally, in Fig. 2.7, the performance of the two blind detectors is plotted as a function of the number of users K . As expected from (2.132), the performance gain offered by the subspace detector is significant for smaller values of K , and the gain diminishes as K increases to N . Moreover, it is seen that the performance of the DMI blind detector is insensitive to K . Figure 2.3. Average output SINR versus SNR and r for two blind detectors. N = 16, K = 6, M = 150. The upper curve in the high-SNR region represents the performance of the subspace blind detector. Figure 2.4. Average output SINR versus r for two blind detectors. N = 16, K = 6, M = 150, SNR = 15 dB. Figure 2.5. Average output SINR versus SNR for two blind detectors. N = 16, K = 6, M = 150, r = 0.4. Figure 2.6. Average output SINR versus the number of signal samples M for two blind detectors. N = 16, K = 6, r = 0.4, SNR = 15 dB. Figure 2.7. Average output SINR versus the number of users K for two blind detectors. N = 16, M = 150, r = 0.4, SNR = 15 dB. Simulation ExamplesWe consider a system with K = 11 users. The users' spreading sequences are randomly generated with processing gain N = 13. All users have the same amplitudes. Figure 2.8 shows both the analytical and simulated SINR performance for the DMI blind detector and the subspace blind detector. For each detector the SINR is plotted as a function of the number of signal samples ( M ) used for estimating the detector at some fixed SNR. The simulated and analytical BER performance of these estimated detectors is shown in Fig. 2.9. The analytical BER performance is evaluated using the approximation Equation 2.149 which effectively treats the output interference plus noise of the estimated detector as having a Gaussian distribution. This can be viewed as a generalization of the results in [386], where it is shown that the output of an exact linear MMSE detector is well approximated with a Gaussian distribution. From Figs. 2.8 and 2.9 it is seen that the agreement between the analytical performance assessment and the simulation results is excellent for both the SINR and BER. The mismatch between analytical and simulation performance occurs for small values of M , which is not surprising since the analytical performance is based on an asymptotic analysis. Figure 2.8. Output average SINR versus the number of signal samples M for DMI and subspace detectors. N = 13, K = 11. The solid line is the analytical performance, and the dashed line is the simulation performance. Figure 2.9. BER versus the number of signal samples M for DMI and subspace detectors. N = 13, K = 11. The solid line is the analytical performance, and the dashed line is the simulation performance. Finally, we note that although in this section we treated only the performance analysis of blind multiuser detection algorithms in simple real-valued synchronous CDMA systems, the analysis for the more realistic complex-valued asynchronous CDMA with multipath channels and blind channel estimation can be found in [196]. Some upper bounds on the achievable performance of various blind multiuser detectors are obtained in [192, 195]. Furthermore, large-system asymptotic performance analysis of blind multiuser detection algorithms is given in [604]. |
EAN: 2147483647
Pages: 91
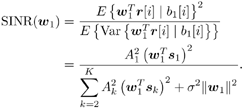
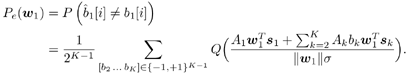
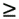
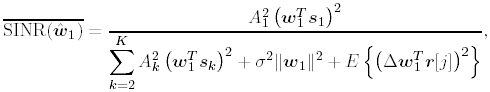
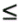
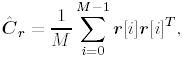
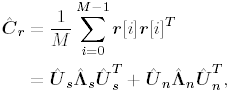
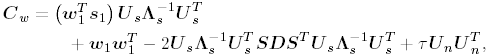
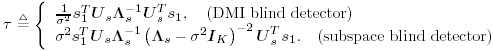
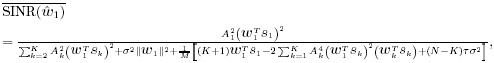
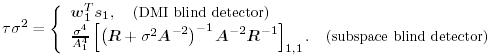
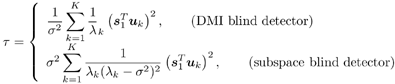
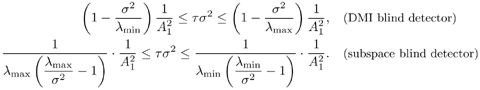
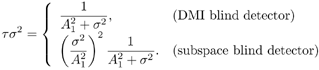
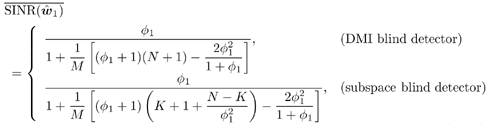
 l
l