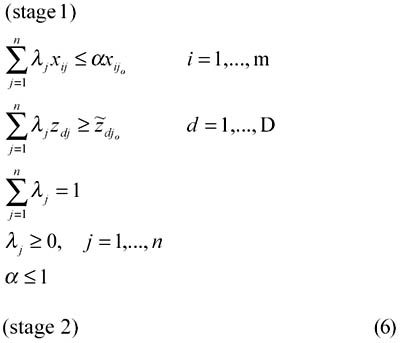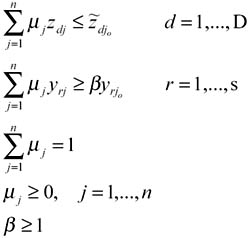THE MODEL

data mining: opportunities and challenges

Chapter XVII - Data Mining in Information Technology and Banking Performance
Data Mining: Opportunities and Challenges
by John Wang (ed)
Idea Group Publishing 2003


	Brought to you by Team-Fly

Consider the indirect impact of IT on banking performance where IT directly impacts certain intermediate measures which in turn are transformed to realize banking performance. Figure 2 describes the indirect impact of IT on banking performance where the first stage use inputs x_i (i =1, , m) to produce outputs z_d ( d = 1, , D), and then these z_d are used as inputs in the second stage to produce outputs y_r (r = 1, , s). It can be seen that z_d (intermediate measures) are outputs in stage 1 and inputs in stage 2. The first stage is viewed as an IT-related, value-added activity where deposit is generated and then used as the input to the second stage where revenue is generated.

Based upon Chen and Zhu (2001), we have

min w₁α + w₂β

where w₁ and w₂ are user-specified weights reflecting the preference over the two stages' performance, and symbol "∼" represents unknown decision variables.

The rationale of model (6) is as follows: (i) when we evaluate the impact of IT investment on the intermediate measures, we want to minimize the input usage given the intermediate measures. For example, given the deposits generated, our objective is to examine whether a bank can reduce its input consumption (including IT investment) compared to the best practice, and (ii) when we evaluate bank performance as a result of the intermediate measures, we want to maximize the performance given the intermediate measures. For example, given the deposits it generated, our objective is to examine whether a bank can increase its profit. Model (6) characterizes the indirect impact of IT on banking performance in a single linear programming problem.

Theorem 1 If α^* = β ^* = 1, then there must exist an optimal solution such that λ^*_{j_o} = μ^*_{j_o} = 1, where (*) represents optimal value in model (6).

[Proof]: Note that λ^*_{j_o} = μ^*_{j_o} = 1, α^*=β^*=1, and are feasible solutions in model (6). This completes the proof. ▪

Theorem 2 If α^* = β^* = 1, then θ^* = 1 and Φ^* = 1, where θ^* and Φ^* are the optimal values to models (2) and (3), respectively.

[Proof]: Suppose α^* = β ^* = 1 in model (6). By Theorem 1, we know that λ^*_{j_o} = μ^*_{j_o} = 1, α^*=β^*=1, and . Now, if θ^* < 1 and Φ^* > 1, then this indicates that α^* = β^* = 1 is not optimal in model (6). A contradiction. ▪

Theorem 2 indicates if α^* = β ^* = 1, the value-chain achieves efficient performance when the two-stage process is viewed as a whole.

If α^* = 1 and β ^* > 1 (or α^* < 1 and β ^* = 1), then model (6) indicates that one of the stages can achieve 100% efficiency given a set of optimal intermediate measures. In this case, the original DEA models (2) and (3) can be used to provide additional information.

From Theorem 2, we immediately have the following result:

Corollary A bank must be a frontier point in both stages with respect to , and β^*y_{rj_o} (r= 1, , s), where (*) represents optimal value in model (6).

Based upon the above Corollary, model (6) yields directions for achieving the best practice of this two-stage process. Consequently, we can study the marginal impact of IT investment on banking performance by using returns to scale estimation discussed in Seiford and Zhu (1999) (see Chen & Zhu, 2001, for such a study).

In model (6), the intermediate measures for a specific bank under evaluation are set as unknown decision variables, . As a result, additional constraints can be imposed on the intermediate measures. This can further help in correctly characterizing the indirect impact of IT on banking performance.


	Brought to you by Team-Fly