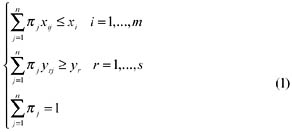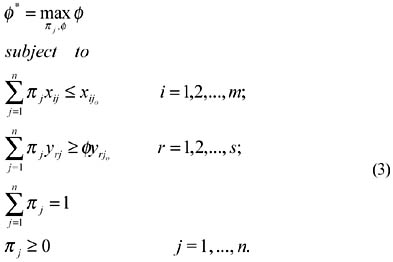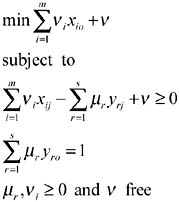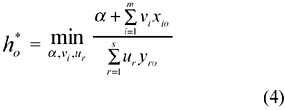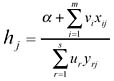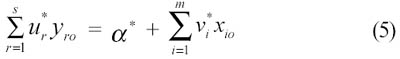DATA ENVELOPMENT ANALYSIS

Chapter XVII - Data Mining in Information Technology and Banking Performance
Data Mining: Opportunities and Challenges
by John Wang (ed)
Idea Group Publishing 2003

	Brought to you by Team-Fly

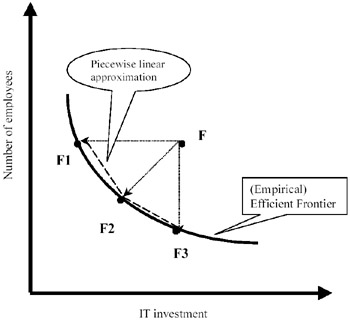
DEA is a mathematical programming approach developed to evaluate the relative efficiency of a set of units that have multiple performance measures inputs and outputs (Charnes, Cooper, & Rhodes, 1978). DEA is particularly useful when the relationship among the multiple performance measures are unknown. Through the optimization for each individual unit, DEA yields an efficient frontier or tradeoff curve that represents the relations among the multiple performance measures.

For example, consider the tradeoff between IT investment and the number of bank employees. Figure 1 illustrates the efficient frontier or tradeoff curve containing F1, F2, and F3 and the area dominated by the curve. A bank's performance (or IT investment strategy) on the efficient frontier is non-dominated (efficient) in the sense that there exists no performance that is strictly better in both IT investment and employee. Through performance evaluation, the efficient frontier that represents the best practice is identified, and any current inefficient performance (e.g., point F) can be improved onto the efficient frontier with suggested directions (to F1, F2, F3, or other points along the curve) (see Figure 1).

Figure 1: Efficient frontier.

Suppose we have n observations on a set of banks; i.e., we have observed input and output values of x_ij (i =1, , m) and y_rj (r =1, , s) for bank j, respectively, where j = 1, , n. The (empirical) efficient frontier is formed by these n observations. The following two properties ensure that we have a piecewise linear approximation to the efficient frontier and the area dominated by the frontier (Banker, Charnes, & Cooper, 1984).

• Property 1. Convexity. and are possible inputs and outputs achievable by the banks, where π_j (j =1, , n) are non-negative scalars such that

• Property 2. Inefficiency. The same y_rj can be obtained by using , where (i.e., the same outputs can be produced by using more inputs). The same x_ij can be used to obtain , where (i.e., the same inputs can be used to produce less outputs).

Consider Figure 1 where the IT investment and the number of employees represent two inputs. Applying Property 1 to F1, F2, and F3 yields a piecewise linear approximation to the curve in Figure 1. Applying both properties expands the line segments F1F2 and F2F3 into the area dominated by the curve.

Applying the above two properties to specific inputs of x_i (i =1, , m) and outputs of y_r (r =1, , s) yields

The DEA efficient frontier is determined by the non-dominated observations satisfying (1). Based upon (1), we have the following DEA model:

where x_ijo is the ith input and y_rjo is the rth output of the j_oth bank (observation) under evaluation.

If θ^* = 1, then the j_oth bank is located on the frontier (or efficient). Otherwise if θ^* < 1, then the j_oth bank is inefficient. Model (2) is called input-oriented DEA model where the goal is to minimize input usage while keeping the outputs at their current levels. Similarly, we can have an output-oriented DEA model where the goal is to maximize the output production while keeping the inputs at their current levels.

Both models (2) and (3) identify the same efficient frontier, because θ^* = 1 if and only if Φ^* = 1. To further illustrate the DEA methodology, we consider dual program of model (3)

The above model is equivalent to

Subject to

Let . Then the model (4) seeks to determine the relative efficiency of each bank. It is clear from the model (4) that smaller value of h_o^* is preferred since we prefer larger values of y_ro and smaller values of x_io. Therefore, model (4) tries to find a set of weights v_i and u_r so that the ratio of aggregated x_io to aggregated y_ro reaches the minimum. Note that model (4) is solved for each bank. Therefore, model (4) does not seek the average best performance, but the efficient or best performance achievable by a proper set of optimized weights.

Note that when h_o^* = 1, we have

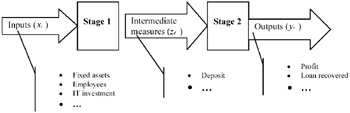
where (*) represents the optimal values in model (4). It can be seen that (5) is similar to the regression model with α^* the intercept on the y-axis. The implicit difference between model (4) and the regression model lies in the fact that (i) model (4) deals with more than one dependent variables (y_rj) at the same time, and (ii) equation (5) is obtained for each bank with a score of one. Further, (5) represents the efficient frontier. Since different units with score of one in model (4) may not be on the same frontier, the resulting efficient frontier is a piecewise linear one, as shown in Figure 1.

From the above discussion, we can see that DEA can be an excellent data-mining approach with respect to extracting efficiency information from the performance data.

Consider three two-stage bank operations as presented in Table 1, where the first stage has two inputs (IT investment and labor) and one output (deposit), and the second stage has one input (deposit generated from the first stage) and one output (profit) (see, e.g., Figure 2).

Table 1: Numerical example

Stage 1 Stage 2					Efficiency
Bank IT	Investment	Labor	Deposit	Profit	Stage1	Stage2	Overall
A	7	9	4	16	1	0.75	1
B	9	4	6	14	1	0.5	1
C	11	6	3	23	0.791	1	1

Figure 2: IT impact on banking performance.

Applying model (2) to the two stages indicates that the banks A and B in the first stage, and bank C in the second stage are efficient. Now, if we ignore the intermediate measure of deposit and apply model (2), the last column of Table 1 indicates that all banks are efficient.

This simple numerical example indicates that the conventional DEA fails to correctly characterize the performance of two-stage operations, since an overall DEA efficient performance does not necessarily indicate efficient performance in individual component. Consequently, improvement to the best practice can be distorted, i.e., the performance improvement of one stage affects the efficiency status of the other because of the presence of intermediate measures. In the next section, we present a DEA model that can directly evaluate the performance of two-stage operations, and set performance targets for intermediate measures.

	Brought to you by Team-Fly