Solving Right Triangles

A right triangle has six components: three sides and three angles. Figure 10-1 shows a right triangle with its various parts labeled. Angles are labeled A, B, and C; sides are labeled Hypotenuse, Base, and Height. Angle C is always 90 degrees (or PI/2 radians). If you know any two of these components (excluding Angle C, which is always known), you can use formulas to solve for the others.

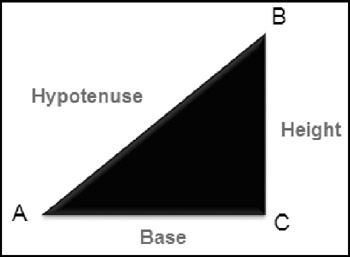
Figure 10-1: A right triangle's components.

The Pythagorean theorem states that

 Height^2 + Base^2 = Hypotenuse^2 

Therefore, if you know two sides of a right triangle, you can calculate the remaining side. The formula to calculate a right triangle's height (given the length of the hypotenuse and base) is as follows:

 =SQRT((hypotenuse^2)-(base^2)) 

The formula to calculate a right triangle's base (given the length of the hypotenuse and height) is as follows:

 =SQRT((hypotenuse^2)-(height^2)) 

The formula to calculate a right triangle's hypotenuse (given the length of the base and height) is as follows:

 =SQRT((height^2)+(base^2)) 

Other useful trigonometric identities are

 SIN(A) = Height/Hypotenuse SIN(B) = Base/Hypotenuse COS(A) = Base/Hypotenuse COS(B) = Height/Hypotenuse TAN(A) = Height/Base SIN(A) = Base/Height 

Note 

Excel's trigonometric functions all assume that the angle arguments are in radians. To convert degrees to radians, use the RADIANS function. To convert radians to degrees, use the DEGREES function.

If you know the height and base, you can use the following formula to calculate the angle formed by the hypotenuse and base (angle A).

 =ATAN(height/base) 

The preceding formula returns radians. To convert to degrees, use this formula:

 =DEGREES(ATAN(height/base)) 

If you know the height and base, you can use the following formula to calculate the angle formed by the hypotenuse and height (angle B):

 =PI()/2-ATAN(height/base) 

The preceding formula returns radians. To convert to degrees, use this formula:

 =90-DEGREES(ATAN(height/base)) 

On the CD 

The companion CD-ROM contains a workbook,  solve right triangle.xlsm, with formulas that calculate various parts of a right triangle, given two known parts. These formulas give you some insight on working with right triangles. The workbook uses a simple VBA macro to enable you to specify the known parts of the triangle.

Figure 10-2 shows a workbook containing formulas to calculate the various parts of a right triangle.

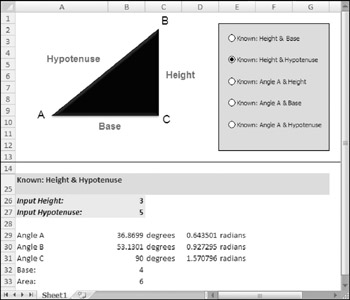
Figure 10-2: This workbook is useful for working with right triangles.