The Characteristics of Markov Analysis
| Markov analysis can be used to analyze a number of different decision situations; however, one of its most popular applications has been the analysis of customer brand switching. This is basically a marketing application that focuses on the loyalty of customers to a particular product brand, store, or supplier. Markov analysis provides information on the probability of customers' switching from one brand to one or more other brands. An example of the brand-switching problem will be used to demonstrate Markov analysis. The brand-switching problem analyzes the probability of customers' changing brands of a product over time. A small community has two gasoline service stations, Petroco and National. The residents of the community purchase gasoline at the two stations on a monthly basis. The marketing department of Petroco surveyed a number of residents and found that the customers were not totally loyal to either brand of gasoline. Customers were willing to change service stations as a result of advertising, service, and other factors. The marketing department found that if a customer bought gasoline from Petroco in any given month, there was only a .60 probability that the customer would buy from Petroco the next month and a .40 probability that the customer would buy gas from National the next month. Likewise, if a customer traded with National in a given month, there was an .80 probability that the customer would purchase gasoline from National in the next month and a .20 probability that the customer would purchase gasoline from Petroco. These probabilities are summarized in Table F.1. Table F.1. Probabilities of Customer Movement per Month
This example contains several important assumptions. First , notice that in Table F.1 the probabilities in each row sum to one because they are mutually exclusive and collectively exhaustive. This means that if a customer trades with Petroco one month, the customer must trade with either Petroco or National the next month (i.e., the customer will not give up buying gasoline, nor will the customer trade with both in one month). Second , the probabilities in Table F.1 apply to every customer who purchases gasoline. Third , the probabilities in Table F.1 will not change over time. In other words, regardless of when the customer buys gasoline, the probabilities of trading with one of the service stations the next month will be the values in Table F.1 The probabilities in Table F.1 will not change in the future if conditions remain the same. Markov assumptions: (1) the probabilities of moving from a state to all others sum to one, (2) the probabilities apply to all system participants , and (3) the probabilities are constant over time. It is these properties that make this example a Markov process. In Markov terminology, the service station a customer trades at in a given month is referred to as a state of the system . Thus, this example contains two states of the system a customer will purchase gasoline at either Petroco or National in any given month. The probabilities of the various states in Table F.1 are known as transition probabilities. In other words, they are the probabilities of a customer's making the transition from one state to another during one time period. Table F.1 contains four transition probabilities. The state of the system is where the system is at a point in time. A transition probability is the probability of moving from one state to another during one time period. The properties for the service station example just described define a Markov process. They are summarized in Markov terminology as follows :
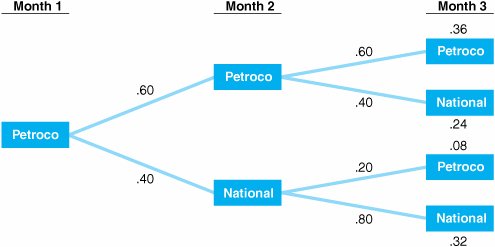
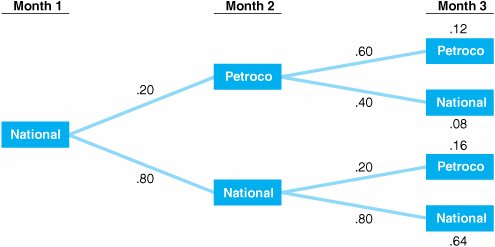
Summary of Markov properties. Markov Analysis InformationNow that we have defined a Markov process and determined that our example exhibits the Markov properties, the next question is "What information will Markov analysis provide?" The most obvious information available from Markov analysis is the probability of being in a state at some future time period, which is also the sort of information we can gain from a decision tree . For example, suppose the service stations wanted to know the probability that a customer would trade with it in month 3, given that the customer trades with it this month (1). This analysis can be performed for each service station by using decision trees, as shown in Figures F.1 and F.2. Figure F.1. Probabilities of future states, given that a customer trades with Petroco this month Figure F.2. Probabilities of future states, given that a customer trades with National this month To determine the probability of a customer's trading with Petroco in month 3, given that the customer initially traded with Petroco in month 1, we must add the two branch probabilities in Figure F.1 associated with Petroco: .36 + .08 = .44, the probability of a customer's trading with Petroco in month 3 Likewise, to determine the probability of a customer's purchasing gasoline from National in month 3, we add the two branch probabilities in Figure F.1 associated with National: .24 + .32 = .56, the probability of a customer's trading with National in month 3 This same type of analysis can be performed under the condition that a customer initially purchased gasoline from National, as shown in Figure F.2. Given that National is the starting state in month 1, the probability of a customer's purchasing gasoline from National in month 3 is .08 + .64 = .72 and the probability of a customer's trading with Petroco in month 3 is .12 + .16 = .28 Notice that for each starting state, Petroco and National, the probabilities of ending up in either state in month 3 sum to one:
Although the use of decision trees is perfectly logical for this type of analysis, it is time consuming and cumbersome. For example, if Petroco wanted to know the probability that a customer who trades with it in month 1 will trade with it in month 10, a rather large decision tree would have to be constructed . Alternatively, the same analysis performed previously using decision trees can be done by using matrix algebra techniques. The future probabilities of being in a state can be determined by using matrix algebra. | |||||||||||||||||||||||||||||
EAN: 2147483647
Pages: 358