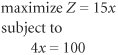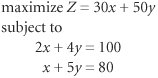Problems | Introduction to Management Science (10th Edition)

[Page 23 ( continued )]

The Willow Furniture Company produces tables. The fixed monthly cost of production is $8,000, and the variable cost per table is $65. The tables sell for $180 apiece.

For a monthly volume of 300 tables, determine the total cost, total revenue, and profit.
Determine the monthly break-even volume for the Willow Furniture Company.

The Retread Tire Company recaps tires. The fixed annual cost of the recapping operation is $60,000. The variable cost of recapping a tire is $9. The company charges $25 to recap a tire.

For an annual volume of 12,000 tires, determine the total cost, total revenue, and profit.
Determine the annual break-even volume for the Retread Tire Company operation.

The Rolling Creek Textile Mill produces denim. The fixed monthly cost is $21,000, and the variable cost per yard of denim is $0.45. The mill sells a yard of denim for $1.30.

For a monthly volume of 18,000 yards of denim, determine the total cost, total revenue, and profit.
Determine the annual break-even volume for the Rolling Creek Textile Mill.

Evergreen Fertilizer Company produces fertilizer. The company's fixed monthly cost is $25,000, and its variable cost per pound of fertilizer is $0.15. Evergreen sells the fertilizer for $0.40 per pound . Determine the monthly break-even volume for the company.

Graphically illustrate the break-even volume for the Retread Tire Company determined in Problem 2.

Graphically illustrate the break-even volume for the Evergreen Fertilizer Company determined in Problem 4.

Andy Mendoza makes handcrafted dolls, which he sells at craft fairs. He is considering mass-producing the dolls to sell in stores. He estimates that the initial investment for plant and equipment will be $25,000, whereas labor, material, packaging, and shipping will be about $10 per doll. If the dolls are sold for $30 each, what sales volume is necessary for Andy to break even?

If the maximum operating capacity of the Retread Tire Company, as described in Problem 2, is 8,000 tires annually, determine the break-even volume as a percentage of that capacity.

[Page 24]

If the maximum operating capacity of the Rolling Creek Textile Mill described in Problem 3 is 25,000 yards of denim per month, determine the break-even volume as a percentage of capacity.

10.

If the maximum operating capacity of Evergreen Fertilizer Company described in Problem 4 is 120,000 pounds of fertilizer per month, determine the break-even volume as a percentage of capacity.

11.

If the Retread Tire Company in Problem 2 changes its pricing for recapping a tire from $25 to $31, what effect will the change have on the break-even volume?

12.

If Evergreen Fertilizer Company in Problem 4 changes the price of its fertilizer from $0.40 per pound to $0.60 per pound, what effect will the change have on the break-even volume?

13.

If Evergreen Fertilizer Company changes its production process to add a weed killer to the fertilizer in order to increase sales, the variable cost per pound will increase from $0.15 to $0.22. What effect will this change have on the break-even volume computed in Problem 12?

14.

If Evergreen Fertilizer Company increases its advertising expenditures by $14,000 per year, what effect will the increase have on the break-even volume computed in Problem 13?

15.

Pastureland Dairy makes cheese, which it sells at local supermarkets. The fixed monthly cost of production is $4,000, and the variable cost per pound of cheese is $0.21. The cheese sells for $0.75 per pound; however, the dairy is considering raising the price to $0.95 per pound. The dairy currently produces and sells 9,000 pounds of cheese per month, but if it raises its price per pound, sales will decrease to 5,700 pounds per month. Should the dairy raise the price?

16.

For the doll-manufacturing enterprise described in Problem 7, Andy Mendoza has determined that $10,000 worth of advertising will increase sales volume by 400 dolls. Should he spend the extra amount for advertising?

17.

Andy Mendoza in Problem 7 is concerned that the demand for his dolls will not exceed the break-even point. He believes he can reduce his initial investment by purchasing used sewing machines and fewer machines. This will reduce his initial investment from $25,000 to $17,000. However, it will also require his employees to work more slowly and perform more operations by hand, thus increasing variable cost from $10 to $14 per doll. Will these changes reduce his break-even point?

18.

The General Store at State University is an auxiliary bookstore located near the dormitories that sells academic supplies , toiletries, sweatshirts and T-shirts, magazines, packaged food items, and canned soft drinks and fruit drinks. The manager of the store has noticed that several pizza delivery services near campus make frequent deliveries. The manager is therefore considering selling pizza at the store. She could buy premade frozen pizzas and heat them in an oven. The cost of the oven and freezer would be $27,000. The frozen pizzas cost $3.75 each to buy from a distributor and to prepare (including labor and a box). To be competitive with the local delivery services, the manager believes she should sell the pizzas for $8.95 apiece. The manager needs to write up a proposal for the university's director of auxiliary services.

Determine how many pizzas would have to be sold to break even.
If The General Store sells 20 pizzas per day, how many days would it take to break even?
The manager of the store anticipates that once the local pizza delivery services start losing business, they will react by cutting prices. If after a month (30 days) the manager has to lower the price of a pizza to $7.95 to keep demand at 20 pizzas per day, as she expects, what will the new break-even point be, and how long will it take the store to break even?

19.

Kim Davis has decided to purchase a cellular phone, but she is unsure about which rate plan to select. The "regular" plan charges a fixed fee of $55 per month for 1,000 minutes of airtime plus $0.33 per minute for any time over 1,000 minutes. The "executive" plan charges a fixed fee of $100 per month for 1,200 minutes of airtime plus $0.25 per minute over 1,200 minutes.

[Page 25]
If Kim expects to use the phone for 21 hours per month, which plan should she select?
At what level of use would Kim be indifferent between the two plans?

20.

Annie McCoy, a student at Tech, plans to open a hot dog stand inside Tech's football stadium during home games. There are seven home games scheduled for the upcoming season. She must pay the Tech athletic department a vendor's fee of $3,000 for the season. Her stand and other equipment will cost her $4,500 for the season . She estimates that each hot dog she sells will cost her $0.35. She has talked to friends at other universities who sell hot dogs at games . Based on their information and the athletic department's forecast that each game will sell out, she anticipates that she will sell approximately 2,000 hot dogs during each game.

What price should she charge for a hot dog in order to break even?
What factors might occur during the season that would alter the volume sold and thus the break-even price Annie might charge?
What price would you suggest that Annie charge for a hot dog to provide her with a reasonable profit while remaining competitive with other food vendors ?

21.

Molly Dymond and Kathleen Taylor are considering the possibility of teaching swimming to kids during the summer. A local swim club opens its pool at noon each day, so it is available to rent during the morning. The cost of renting the pool during the 10-week period for which Molly and Kathleen would need it is $1,700. The pool would also charge Molly and Kathleen an admission, towel service, and life guarding fee of $7 per pupil , and Molly and Kathleen estimate an additional $5 cost per student to hire several assistants. Molly and Kathleen plan to charge $75 per student for the 10-week swimming class.

How many pupils do Molly and Kathleen need to enroll in their class to break even?
If Molly and Kathleen want to make a profit of $5,000 for the summer, how many pupils do they need to enroll?
Molly and Kathleen estimate that they might not be able to enroll more than 60 pupils. If they enroll this many pupils, how much would they need to charge per pupil in order to realize their profit goal of $5,000?

22.

The College of Business at Tech is planning to begin an online MBA program. The initial start-up cost for computing equipment, facilities, course development, and staff recruitment and development is $350,000. The college plans to charge tuition of $18,000 per student per year. However, the university administration will charge the college $12,000 per student for the first 100 students enrolled each year for administrative costs and its share of the tuition payments.

How many students does the college need to enroll in the first year to break even?
If the college can enroll 75 students the first year, how much profit will it make?
The college believes it can increase tuition to $24,000, but doing so would reduce enrollment to 35. Should the college consider doing this?

23.

The Star Youth Soccer Club helps to support its 20 boys' and girls ' teams financially , primarily through the payment of coaches. The club puts on a tournament each fall to help pay its expenses. The cost of putting on the tournament is $8,000, mainly for development, printing, and mailing of the tournament brochures . The tournament entry fee is $400 per team. For every team that enters, it costs the club about $75 to pay referees for the three-game minimum each team is guaranteed . If the club needs to clear $60,000 from the tournament , how many teams should it invite?

24.

In the example used to demonstrate model construction in this chapter (p. 4), a firm sells a product, x , for $20 that costs $5 to make, it has 100 pounds of steel to make the product, and it takes 4 pounds of steel to make each unit. The model that was constructed is

[Page 26]

Now suppose that there is a second product, y , that has a profit of $10 and requires 2 pounds of steel to make, such that the model becomes

Can you determine a solution to this new model that will achieve the objective? Explain your answer.

25.

Consider a model in which two products, x and y , are produced. There are 100 pounds of material and 80 hours of labor available. It requires 2 pounds of material and 1 hour of labor to produce a unit of x , and 4 pounds of material and 5 hours of labor to produce a unit of y . The profit for x is $30 per unit, and the profit for y is $50 per unit. If we want to know how many units of x and y to produce to maximize profit, the model is

Determine the solution to this problem and explain your answer.

26.

The Easy Drive Car Rental Agency needs 500 new cars in its Nashville operation and 300 new cars in Jacksonville, and it currently has 400 new cars in both Atlanta and Birmingham. It costs $30 to move a car from Atlanta to Nashville, $70 to move a car from Atlanta to Jacksonville, $40 to move a car from Birmingham to Nashville, and $60 to move a car from Birmingham to Jacksonville. The agency wants to determine how many cars should be transported from the agencies in Atlanta and Birmingham to the agencies in Nashville and Jacksonville in order to meet demand while minimizing the transport costs. Develop a mathematical model for this problem and use logic to determine a solution.

27.

Ed Norris has developed a Web site for his used textbook business at State University. To sell advertising he needs to forecast the number of site visits he expects in the future. For the past 6 months he has had the following number of site visits :

Month	1	2	3	4	5	6
Site visits	6,300	10,200	14,700	18,500	25,100	30,500

Determine a forecast for Ed to use for month 7 and explain the logic used to develop your forecast.

28.

When Marie McCoy wakes up on Saturday morning, she remembers that she had promised the PTA she would make some cakes and/or homemade bread for its bake sale that afternoon. However, she does not have time to go to the store and get ingredients , and she has only a short time to bake things in her oven. Because cakes and breads require different baking temperatures , she cannot bake them simultaneously , and she has only 3 hours available to bake. A cake requires 3 cups of flour, and a loaf of bread requires 8 cups; Marie has 20 cups of flour. A cake requires 45 minutes to bake, and a loaf of bread requires 30 minutes. The PTA will sell a cake for $10 and a loaf of bread for $6. Marie wants to decide how many cakes and loaves of bread she should make. Identify all the possible solutions to this problem (i.e., combinations of cakes and loaves of bread Marie has the time and flour to bake) and select the best one.