Decision Making Without Probabilities
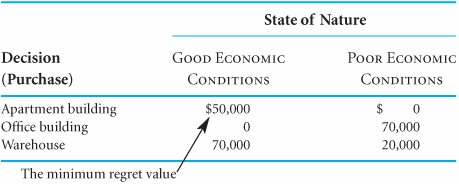
| The following example will illustrate the development of a payoff table without probabilities. An investor is to purchase one of three types of real estate, as illustrated in Figure 12.1. The investor must decide among an apartment building, an office building, and a warehouse. The future states of nature that will determine how much profit the investor will make are good economic conditions and poor economic conditions. The profits that will result from each decision in the event of each state of nature are shown in Table 12.2. Figure 12.1. Decision situation with real estate investment alternatives(This item is displayed on page 516 in the print version) Table 12.2. Payoff table for the real estate investments
Decision-Making CriteriaOnce the decision situation has been organized into a payoff table, several criteria are available for making the actual decision. These decision criteria, which will be presented in this section, include maximax, maximin, minimax regret , Hurwicz, and equal likelihood . On occasion these criteria will result in the same decision; however, often they will yield different decisions. The decision maker must select the criterion or combination of criteria that best suits his or her needs. The Maximax CriterionWith the maximax criterion , the decision maker selects the decision that will result in the maximum of the maximum payoffs. (In fact, this is how this criterion derives its namea maximum of a maximum.) The maximax criterion is very optimistic. The decision maker assumes that the most favorable state of nature for each decision alternative will occur. Thus, for example, using this criterion, the investor would optimistically assume that good economic conditions will prevail in the future. The maximax criterion results in the maximum of the maximum payoffs . The maximax criterion is applied in Table 12.3. The decision maker first selects the maximum payoff for each decision. Notice that all three maximum payoffs occur under good economic conditions. Of the three maximum payoffs$50,000, $100,000, and $30,000the maximum is $100,000; thus, the corresponding decision is to purchase the office building. Table 12.3. Payoff table illustrating a maximax decision Although the decision to purchase an office building will result in the largest payoff ($100,000), such a decision completely ignores the possibility of a potential loss of $40,000. The decision maker who uses the maximax criterion assumes a very optimistic future with respect to the state of nature.
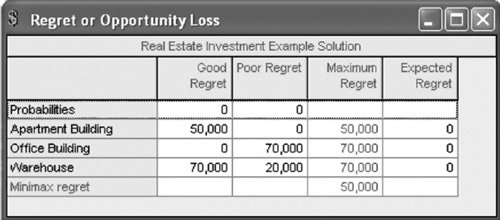
Before the next criterion is presented, it should be pointed out that the maximax decision rule as presented here deals with profit . However, if the payoff table consisted of costs, the opposite selection would be indicated: the minimum of the minimum costs, or a minimin criterion. For the subsequent decision criteria we encounter, the same logic in the case of costs can be used. The Maximin CriterionIn contrast to the maximax criterion, which is very optimistic, the maximin criterion is pessimistic. With the maximin criterion, the decision maker selects the decision that will reflect the maximum of the minimum payoffs. For each decision alternative, the decision maker assumes that the minimum payoff will occur. Of these minimum payoffs, the maximum is selected. The maximin criterion for our investment example is demonstrated in Table 12.4. Table 12.4. Payoff table illustrating a maximin decision The maximin criterion results in the maximum of the minimum payoff . The minimum payoffs for our example are $30,000, $40,000, and $10,000. The maximum of these three payoffs is $30,000; thus, the decision arrived at by using the maximin criterion would be to purchase the apartment building. This decision is relatively conservative because the alternatives considered include only the worst outcomes that could occur. The decision to purchase the office building as determined by the maximax criterion includes the possibility of a large loss ($40,000). The worst that can occur from the decision to purchase the apartment building, however, is a gain of $30,000 . On the other hand, the largest possible gain from purchasing the apartment building is much less than that of purchasing the office building (i.e., $50,000 vs. $100,000). If Table 12.4 contained costs instead of profits as the payoffs, the conservative approach would be to select the maximum cost for each decision. Then the decision that resulted in the minimum of these costs would be selected. The Minimax Regret CriterionIn our example, suppose the investor decided to purchase the warehouse, only to discover that economic conditions in the future were better than expected. Naturally, the investor would be disappointed that she had not purchased the office building because it would have resulted in the largest payoff ($100,000) under good economic conditions. In fact, the investor would regret the decision to purchase the warehouse, and the degree of regret would be $70,000 , the difference between the payoff for the investor's choice and the best choice. Regret is the difference between the payoff from the best decision and all other decision payoffs . This brief example demonstrates the principle underlying the decision criterion known as minimax regret criterion . With this decision criterion, the decision maker attempts to avoid regret by selecting the decision alternative that minimizes the maximum regret. The minimax regret criterion minimizes the maximum regret . To use the minimax regret criterion, a decision maker first selects the maximum payoff under each state of nature. For our example, the maximum payoff under good economic conditions is $100,000, and the maximum payoff under poor economic conditions is $30,000. All other payoffs under the respective states of nature are subtracted from these amounts, as follows :
These values represent the regret that the decision maker would experience if a decision were made that resulted in less than the maximum payoff. The values are summarized in a modified version of the payoff table known as a regret table , shown in Table 12.5. (Such a table is sometimes referred to as an opportunity loss table , in which case the term opportunity loss is synonymous with regret .) Table 12.5. Regret table
To make the decision according to the minimax regret criterion, the maximum regret for each decision must be determined. The decision corresponding to the minimum of these regret values is then selected. This process is illustrated in Table 12.6. Table 12.6. Regret table illustrating the minimax regret decision According to the minimax regret criterion, the decision should be to purchase the apartment building rather than the office building or the warehouse. This particular decision is based on the philosophy that the investor will experience the least amount of regret by purchasing the apartment building. In other words, if the investor purchased either the office building or the warehouse, $70,000 worth of regret could result; however, the purchase of the apartment building will result in, at most, $50,000 in regret. The Hurwicz Criterion The Hurwicz criterion strikes a compromise between the maximax and maximin criteria. The principle underlying this decision criterion is that the decision maker is neither totally optimistic (as the maximax criterion assumes) nor totally pessimistic (as the maximin criterion assumes). With the Hurwicz criterion, the decision payoffs are weighted by a coefficient of optimism , a measure of the decision maker's optimism. The coefficient of optimism, which we will define as a, is between zero and one (i.e., 0 The Hurwicz criterion is a compromise between the maximax and maximin criteria . The coefficient of optimism, a , is a measure of the decision maker's optimism . The Hurwicz criterion requires that, for each decision alternative, the maximum payoff be multiplied by a and the minimum payoff be multiplied by 1 - a . For our investment example, if a equals .4 (i.e., the investor is slightly pessimistic), 1 - a = .6, and the following values will result:
The Hurwicz criterion multiplies the best payoff by a , the coefficient of optimism, and the worst payoff by 1 - a , for each decision, and the best result is selected . The Hurwicz criterion specifies selection of the decision alternative corresponding to the maximum weighted value, which is $38,000 for this example. Thus, the decision would be to purchase the apartment building. It should be pointed out that when a = 0, the Hurwicz criterion is actually the maximin criterion; when a = 1.0, it is the maximax criterion. A limitation of the Hurwicz criterion is the fact that a must be determined by the decision maker. It can be quite difficult for a decision maker to accurately determine his or her degree of optimism. Regardless of how the decision maker determines a , it is still a completely subjective measure of the decision maker's degree of optimism. Therefore, the Hurwicz criterion is a completely subjective decision-making criterion. The Equal Likelihood CriterionWhen the maximax criterion is applied to a decision situation, the decision maker implicitly assumes that the most favorable state of nature for each decision will occur. Alternatively, when the maximin criterion is applied, the least favorable states of nature are assumed. The equal likelihood , or LaPlace, criterion weights each state of nature equally, thus assuming that the states of nature are equally likely to occur. The equal likelihood criterion multiplies the decision payoff for each state of nature by an equal weight . Because there are two states of nature in our example, we assign a weight of .50 to each one. Next, we multiply these weights by each payoff for each decision:
As with the Hurwicz criterion, we select the decision that has the maximum of these weighted values. Because $40,000 is the highest weighted value, the investor's decision would be to purchase the apartment building. In applying the equal likelihood criterion, we are assuming a 50% chance, or .50 probability, that either state of nature will occur. Using this same basic logic, it is possible to weight the states of nature differently (i.e., unequally) in many decision problems. In other words, different probabilities can be assigned to each state of nature, indicating that one state is more likely to occur than another. The application of different probabilities to the states of nature is the principle behind the decision criteria to be presented in the section on expected value. Summary of Criteria ResultsThe decisions indicated by the decision criteria examined so far can be summarized as follows:
The decision to purchase the apartment building was designated most often by the various decision criteria. Notice that the decision to purchase the warehouse was never indicated by any criterion. This is because the payoffs for an apartment building, under either set of future economic conditions, are always better than the payoffs for a warehouse. Thus, given any situation with these two alternatives (and any other choice, such as purchasing the office building), the decision to purchase an apartment building will always be made over the decision to purchase a warehouse. In fact, the warehouse decision alternative could have been eliminated from consideration under each of our criteria. The alternative of purchasing a warehouse is said to be dominated by the alternative of purchasing an apartment building. In general, dominated decision alternatives can be removed from the payoff table and not considered when the various decision-making criteria are applied. This reduces the complexity of the decision analysis somewhat. However, in our discussions throughout this chapter of the application of decision criteria, we will leave the dominated alternative in the payoff table for demonstration purposes. A dominant decision is one that has a better payoff than another decision under each state of nature . The use of several decision criteria often results in a mix of decisions, with no one decision being selected more than the others. The criterion or collection of criteria used and the resulting decision depend on the characteristics and philosophy of the decision maker. For example, the extremely optimistic decision maker might eschew the majority of the foregoing results and make the decision to purchase the office building because the maximax criterion most closely reflects his or her personal decision-making philosophy. The appropriate criterion is dependent on the risk personality and philosophy of the decision maker . Solution of Decision-Making Problems Without Probabilities with QM for WindowsQM for Windows includes a module to solve decision analysis problems. QM for Windows will be used to illustrate the use of the maximax, maximin, minimax regret, equal likelihood, and Hurwicz criteria for the real estate problem considered in this section. The problem data are input very easily. A summary of the input and solution output for the maximax, maximin, and Hurwicz criteria is shown in Exhibit 12.1. The decision with the equal likelihood criterion can be determined by using an alpha value for the Hurwicz criterion equal to the equal likelihood weight, which is .5 for our real estate investment example. The solution output with alpha equal to .5 is shown in Exhibit 12.2. The decision with the minimax regret criterion is shown in Exhibit 12.3. Exhibit 12.1.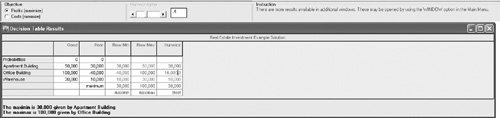 Exhibit 12.2.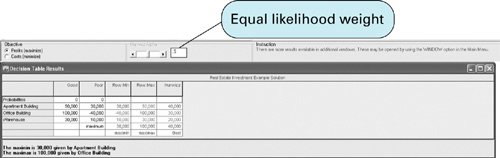 Exhibit 12.3. Solution of Decision-Making Problems Without Probabilities with ExcelExcel can also be used to solve decision analysis problems using the decision-making criteria presented in this section. Exhibit 12.4 illustrates the application of the maximax, minimax, minimax regret, Hurwicz, and equal likelihood criteria for our real estate investment example. Exhibit 12.4. In cell E7 the formula = MAX(C7,D7) selects the maximum payoff outcome for the decision to purchase the apartment building. Next, in cell C11 the maximum of the maximum payoffs is determined with the formula = MAX(E7:E9) . The maximin decision is determined similarly. In the regret table in Exhibit 12.4, in cell C18 the formula =MAX(C7:C9) C7 computes the regret for the apartment building decision under good economic conditions, and then the maximum regret for the apartment building is determined in cell E18, using the formula =MAX(C18,D18) . The minimax regret value is determined in cell C22 with the formula = MIN(E18:E20) . The Hurwicz and equal likelihood decisions are determined using their respective formulas in cells C27:C29 and C32:C34 . | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
EAN: 2147483647
Pages: 358


 1.0). If a = 0, then the decision maker is completely pessimistic. (Given this definition, if a is the coefficient of optimism, 1 - a is the
1.0). If a = 0, then the decision maker is completely pessimistic. (Given this definition, if a is the coefficient of optimism, 1 - a is the