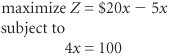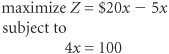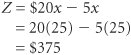The Management Science Approach to Problem Solving

[Page 2 ( continued )]

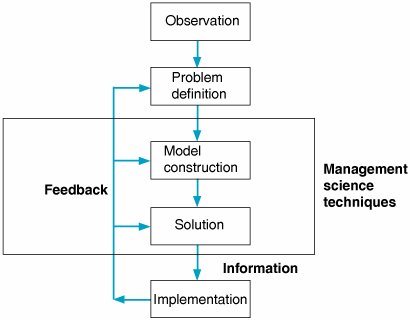
As indicated in the previous section, management science encompasses a logical, systematic approach to problem solving, which closely parallels what is known as the scientific method for attacking problems. This approach, as shown in Figure 1.1, follows a generally recognized and ordered series of steps: (1) observation, (2) definition of the problem, (3) model construction, (4) model solution, and (5) implementation of solution results. We will analyze each of these steps individually.

Figure 1.1. The management science process

(This item is displayed on page 3 in the print version)

The steps of the scientific method are (1) observation, (2) problem definition, (3) model construction, (4) model solution, and (5) implementation .

Observation

The first step in the management science process is the identification of a problem that exists in the system (organization). The system must be continuously and closely observed so that problems can be identified as soon as they occur or are anticipated. Problems are not always the result of a crisis that must be reacted to but, instead, frequently involve an anticipatory or planning situation. The person who normally identifies a problem is the manager because the managers work in places where problems might occur. However, problems can often be identified by a management scientist , a person skilled in the techniques of management science and trained to identify problems, who has been hired specifically to solve problems using management science techniques.

---

[Page 3]

A management scientist is a person skilled in the application of management science techniques .

Definition of the Problem

Once it has been determined that a problem exists, the problem must be clearly and concisely defined . Improperly defining a problem can easily result in no solution or an inappropriate solution. Therefore, the limits of the problem and the degree to which it pervades other units of the organization must be included in the problem definition. Because the existence of a problem implies that the objectives of the firm are not being met in some way, the goals (or objectives) of the organization must also be clearly defined. A stated objective helps to focus attention on what the problem actually is.

Model Construction

A management science model is an abstract representation of an existing problem situation. It can be in the form of a graph or chart, but most frequently a management science model consists of a set of mathematical relationships. These mathematical relationships are made up of numbers and symbols.

A model is an abstract mathematical representation of a problem situation .

As an example, consider a business firm that sells a product. The product costs $5 to produce and sells for $20. A model that computes the total profit that will accrue from the items sold is

Z = $20 x - 5 x

A variable is a symbol used to represent an item that can take on any value .

In this equation x represents the number of units of the product that are sold, and Z represents the total profit that results from the sale of the product. The symbols x and Z are variables . The term variable is used because no set numeric value has been specified for these items. The number of units sold, x , and the profit, Z , can be any amount (within limits); they can vary. These two variables can be further distinguished. Z is a dependent variable because its value is dependent on the number of units sold; x is an independent variable because the number of units sold is not dependent on anything else (in this equation).

---

[Page 4]

Parameters are known, constant values that are often coefficients of variables in equations .

The numbers $20 and $5 in the equation are referred to as parameters . Parameters are constant values that are generally coefficients of the variables (symbols) in an equation. Parameters usually remain constant during the process of solving a specific problem. The parameter values are derived from data (i.e., pieces of information) from the problem environment. Sometimes the data are readily available and quite accurate. For example, presumably the selling price of $20 and product cost of $5 could be obtained from the firm's accounting department and would be very accurate. However, sometimes data are not as readily available to the manager or firm, and the parameters must be either estimated or based on a combination of the available data and estimates. In such cases, the model is only as accurate as the data used in constructing the model.

Data are pieces of information from the problem environment .

The equation as a whole is known as a functional relationship (also called function and relationship) . The term is derived from the fact that profit, Z , is a function of the number of units sold, x , and the equation relates profit to units sold.

A model is a functional relationship that includes variables, parameters, and equations .

Because only one functional relationship exists in this example, it is also the model . In this case the relationship is a model of the determination of profit for the firm. However, this model does not really replicate a problem. Therefore, we will expand our example to create a problem situation.

Let us assume that the product is made from steel and that the business firm has 100 pounds of steel available. If it takes 4 pounds of steel to make each unit of the product, we can develop an additional mathematical relationship to represent steel usage:

4 x = 100 lb. of steel

This equation indicates that for every unit produced, 4 of the available 100 pounds of steel will be used. Now our model consists of two relationships:

We say that the profit equation in this new model is an objective function , and the resource equation is a constraint . In other words, the objective of the firm is to achieve as much profit, Z , as possible, but the firm is constrained from achieving an infinite profit by the limited amount of steel available. To signify this distinction between the two relationships in this model, we will add the following notations:

This model now represents the manager's problem of determining the number of units to produce. You will recall that we defined the number of units to be produced as x . Thus, when we determine the value of x , it represents a potential (or recommended) decision for the manager. Therefore, x is also known as a decision variable . The next step in the management science process is to solve the model to determine the value of the decision variable.

Model Solution

A management science technique usually applies to a specific model type.

Once models have been constructed in management science, they are solved using the management science techniques presented in this text. A management science solution technique usually applies to a specific type of model. Thus, the model type and solution method are both part of the management science technique. We are able to say that a model is solved because the model represents a problem. When we refer to model solution, we also mean problem solution.

---

[Page 5]

Time Out: For Pioneers in Management Science

Throughout this text TIME OUT boxes introduce you to the individuals who developed the various techniques that are described in the chapters. This will provide a historical perspective on the development of the field of management science. In this first instance we will briefly outline the development of management science.

Although a number of the mathematical techniques that make up management science date to the turn of the twentieth century or before, the field of management science itself can trace its beginnings to military operations research (OR) groups formed during World War II in Great Britain circa 1939. These OR groups typically consisted of a team of about a dozen individuals from different fields of science, mathematics, and the military, brought together to find solutions to military- related problems. One of the most famous of these groupscalled "Blackett's circus" after its leader, Nobel laureate P. M. S. Blackett of the University of Manchester and a former naval officerincluded three physiologists, two mathematical physicists, one astrophysicist, one general physicist , two mathematicians, an Army officer, and a surveyor . Blackett's group and the other OR teams made significant contributions in improving Britain's early-warning radar system (which was instrumental in their victory in the Battle of Britain), aircraft gunnery, antisubmarine warfare , civilian defense, convoy size determination, and bombing raids over Germany.

The successes achieved by the British OR groups were observed by two Americans working for the U.S. military, Dr. James B. Conant and Dr. Vannevar Bush, who recommended that OR teams be established in the U.S. branches of the military. Subsequently, both the Air Force and Navy created OR groups.

After World War II the contributions of the OR groups were considered so valuable that the Army, Air Force, and Navy set up various agencies to continue research of military problems. Two of the more famous agencies were the Navy's Operations Evaluation Group at MIT and Project RAND, established by the Air Force to study aerial warfare. Many of the individuals who developed operations research and management science techniques did so while working at one of these agencies after World War II or as a result of their work there.

As the war ended and the mathematical models and techniques that were kept secret during the war began to be released, there was a natural inclination to test their applicability to business problems. At the same time, various consulting firms were established to apply these techniques to industrial and business problems, and courses in the use of quantitative techniques for business management began to surface in American universities. In the early 1950s the use of these quantitative techniques to solve management problems became known as management science, and it was popularized by a book of that name by Stafford Beer of Great Britain.

For the example model developed in the previous section,

the solution technique is simple algebra. Solving the constraint equation for x , we have

Substituting the value of 25 for x into the profit function results in the total profit:

Thus, if the manager decides to produce 25 units of the product and all 25 units sell, the business firm will receive $375 in profit. Note, however, that the value of the decision variable does not constitute an actual decision; rather, it is information that serves as a recommendation or guideline, helping the manager make a decision.

---

[Page 6]

Management Science Application: Management Science at Taco Bell

Taco Bell, an international fast-food chain with annual sales of approximately $4.6 billion, operates more than 6,500 locations worldwide. In the fast-food business the operating objective is, in general, to provide quality food, good service, and a clean environment. Although Taco Bell sees these three attributes as equally important, good service, as measured by its speed, has the greatest impact on revenues .

The 3- hour lunch period 11:00 A.M. to 2:00 P.M. accounts for 52% of Taco Bell's daily sales. Most fast-food restaurants have lines of waiting customers during this period, and so speed of service determines sales capacity. If service time decreases, sales capacity increases, and vice versa. However, as speed of service increases , labor costs also increase. Because very few food items can be prepared in advance and inventoried, products must be prepared when they are ordered, making food preparation very labor intensive . Thus, speed of service depends on labor availability.

Taco Bell research studies showed that when customers are in line up to 5 minutes only, their perception of that waiting time is only a few minutes. However, after waiting time exceeds 5 minutes, customer perception of that waiting time increases exponentially. The longer the perceived waiting time, the more likely the customer is to leave the restaurant without ordering. The company determined that a 3-minute average waiting time would result in only 2.5% of customers leaving. The company believed this was an acceptable level of attrition, and it established this waiting time as its service goal.

To achieve this goal Taco Bell developed a labor-management system based on an integrated set of management science models to forecast customer traffic for every 15-minute interval during the day and to schedule employees accordingly to meet customer demand. This labor-management system includes a forecasting model to predict customer transactions; a simulation model to determine labor requirements based on these transactions; and an integer programming model to schedule employees and minimize payroll. From 1993 through 1997 the labor-management system using these models saved Taco Bell over $53 million.

Source: J. Heuter and W. Swart, "An Integrated Labor-Management System for Taco Bell," Interfaces 28, no. 1 (JanuaryFebruary 1998): 7591.

Some management science techniques do not generate an answer or a recommended decision. Instead, they provide descriptive results : results that describe the system being modeled . For example, suppose the business firm in our example desires to know the average number of units sold each month during a year. The monthly data (i.e., sales) for the past year are as follows:

Month	Sales		Month	Sales
January	30		July	35
February	40		August	50
March	25		September	60
April	60		October	40
May	30		November	35
June	25		December	50
			Total	480 units

A management science solution can be either a recommended decision or information that helps a manager make a decision .

---

[Page 7]

Monthly sales average 40 units (480 · 12). This result is not a decision; it is information that describes what is happening in the system. The results of the management science techniques in this text are examples of the two types shown in this section: (1) solutions/decisions and (2) descriptive results.

Implementation

The final step in the management science process for problem solving described in Figure 1.1 is implementation. Implementation is the actual use of the model once it has been developed or the solution to the problem the model was developed to solve. This is a critical but often overlooked step in the process. It is not always a given that once a model is developed or a solution found, it is automatically used. Frequently the person responsible for putting the model or solution to use is not the same person who developed the model and, thus, the user may not fully understand how the model works or exactly what it is supposed to do. Individuals are also sometimes hesitant to change the normal way they do things or to try new things. In this situation the model and solution may get pushed to the side or ignored altogether if they are not carefully explained and their benefit fully demonstrated. If the management science model and solution are not implemented, then the effort and resources used in their development have been wasted .