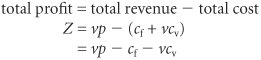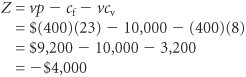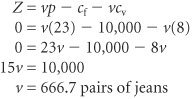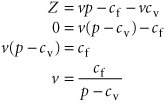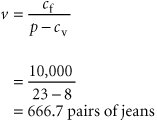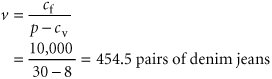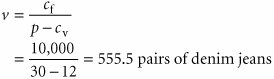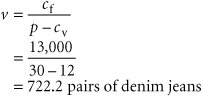Model Building: Break-Even Analysis
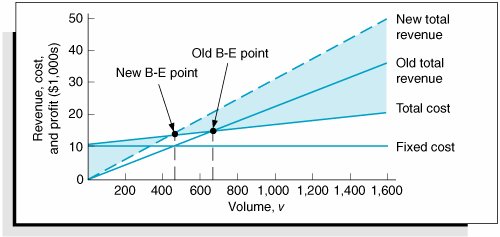
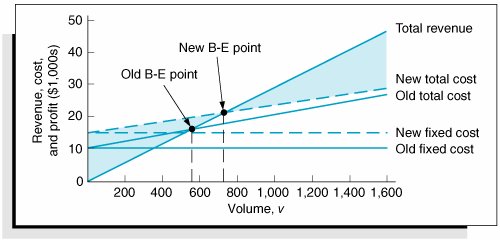
Model Building: Break-Even AnalysisIn the previous section we gave a brief, general description of how management science models are formulated and solved , using a simple algebraic example. In this section we will continue to explore the process of building and solving management science models, using break-even analysis , also called profit analysis . Break-even analysis is a good topic to expand our discussion of model building and solution because it is straightforward, relatively familiar to most people, and not overly complex. In addition, it provides a convenient means to demonstrate the different ways management science models can be solvedmathematically (by hand), graphically, and with a computer. The purpose of break-even analysis is to determine the number of units of a product (i.e., the volume) to sell or produce that will equate total revenue with total cost. The point where total revenue equals total cost is called the break-even point, and at this point profit is zero. The break-even point gives a manager a point of reference in determining how many units will be needed to ensure a profit. Components of Break-Even AnalysisThe three components of break-even analysis are volume, cost, and profit. Volume is the level of sales or production by a company. It can be expressed as the number of units (i.e., quantity) produced and sold, as the dollar volume of sales, or as a percentage of total capacity available. Two type of costs are typically incurred in the production of a product: fixed costs and variable costs. Fixed costs are generally independent of the volume of units produced and sold. That is, fixed costs remain constant, regardless of how many units of product are produced within a given range. Fixed costs can include such items as rent on plant and equipment, taxes, staff and management salaries, insurance, advertising, depreciation, heat and light, plant maintenance, and so on. Taken together, these items result in total fixed costs. Fixed costs are independent of volume and remain constant . Variable costs are determined on a per-unit basis. Thus, total variable costs depend on the number of units produced. Variable costs include such items as raw materials and resources, direct labor, packaging, material handling, and freight. Variable costs depend on the number of items produced . Total variable costs are a function of the volume and the variable cost per unit . This relationship can be expressed mathematically as total variable cost = vc v where c v = variable cost per unit and v = volume (number of units) sold. The total cost of an operation is computed by summing total fixed cost and total variable cost, as follows : total cost = total fixed cost + total variable cost or TC = c f + vc v where c f = fixed cost. Total cost ( TC ) equals the fixed cost ( c f ) plus the variable cost per unit ( c v ) multiplied by volume ( v ) . As an example, consider Western Clothing Company, which produces denim jeans. The company incurs the following monthly costs to produce denim jeans : If we arbitrarily let the monthly sales volume, v , equal 400 pairs of denim jeans, the total cost is TC = c f + vc v = $10,000 + (400)(8) = $13,200 The third component in our break-even model is profit . Profit is the difference between total revenue and total cost. Total revenue is the volume multiplied by the price per unit, total revenue = vp where p = price per unit. Profit is the difference between total revenue (volume multiplied by price) and total cost . For our clothing company example, if denim jeans sell for $23 per pair and we sell 400 pairs per month, then the total monthly revenue is total revenue = vp = (400)(23) = $9,200 Now that we have developed relationships for total revenue and total cost, profit ( Z ) can be computed as follows: Computing the Break-Even PointFor our clothing company example, we have determined total revenue and total cost to be $9,200 and $13,200, respectively. With these values, there is no profit but, instead, a loss of $4,000: total profit = total revenue total cost = $9,200 13,200 = $4,000 We can verify this result by using our total profit formula, Z = vp c f vc v and the values v = 400, p = $23, c f = $10,000, and c v = $8: Obviously, the clothing company does not want to operate with a monthly loss of $4,000 because doing so might eventually result in bankruptcy. If we assume that price is static because of market conditions and that fixed costs and the variable cost per unit are not subject to change, then the only part of our model that can be varied is volume . Using the modeling terms we developed earlier in this chapter, price, fixed costs, and variable costs are parameters, whereas the volume, v , is a decision variable . In break-even analysis we want to compute the value of v that will result in zero profit. The break-even point is the volume (v) that equates total revenue with total cost where profit is zero . At the break-even point , where total revenue equals total cost, the profit, Z , equals zero. Thus, if we let profit, Z , equal zero in our total profit equation and solve for v , we can determine the break-even volume: In other words, if the company produces and sells 666.7 pairs of jeans, the profit (and loss) will be zero and the company will break even . This gives the company a point of reference from which to determine how many pairs of jeans it needs to produce and sell in order to gain a profit (subject to any capacity limitations). For example, a sales volume of 800 pairs of denim jeans will result in the following monthly profit: In general, the break-even volume can be determined using the following formula: For our example, Graphical SolutionIt is possible to represent many of the management science models in this text graphically and use these graphical models to solve problems. Graphical models also have the advantage of providing a "picture" of the model that can sometimes help us understand the modeling process better than the mathematics alone can. We can easily graph the break-even model for our Western Clothing Company example because the functions for total cost and total revenue are linear . That means we can graph each relationship as a straight line on a set of coordinates, as shown in Figure 1.2. Figure 1.2. Break-even model(This item is displayed on page 10 in the print version) In Figure 1.2, the fixed cost, c f , has a constant value of $10,000, regardless of the volume. The total cost line, TC , represents the sum of variable cost and fixed cost. The total cost line increases because variable cost increases as the volume increases. The total revenue line also increases as volume increases , but at a faster rate than total cost. The point where these two lines intersect indicates that total revenue equals total cost. The volume, v , that corresponds to this point is the break-even volume . The break-even volume in Figure 1.2 is 666.7 pairs of denim jeans. Sensitivity AnalysisWe have now developed a general relationship for determining the break-even volume, which was the objective of our modeling process. This relationship enables us to see how the level of profit (and loss) is directly affected by changes in volume. However, when we developed this model, we assumed that our parameters, fixed and variable costs and price, were constant. In reality such parameters are frequently uncertain and can rarely be assumed to be constant, and changes in any of the parameters can affect the model solution. The study of changes on a management science model is called sensitivity analysis that is, seeing how sensitive the model is to changes. Sensitivity analysis can be performed on all management science models in one form or another. In fact, sometimes companies develop models for the primary purpose of experimentation to see how the model will react to different changes the company is contemplating or that management might expect to occur in the future. As a demonstration of how sensitivity analysis works, we will look at the effects of some changes on our break-even model. The first thing we will analyze is price. As an example, we will increase the price for denim jeans from $23 to $30. As expected, this increases the total revenue, and it therefore reduces the break-even point from 666.7 pairs of jeans to 454.5 pairs of jeans: In general, an increase in price lowers the break-even point, all other things held constant . The effect of the price change on break-even volume is illustrated in Figure 1.3. Figure 1.3. Break-even model with an increase in price(This item is displayed on page 11 in the print version) Although a decision to increase price looks inviting from a strictly analytical point of view, it must be remembered that the lower break-even volume and higher profit are possible but not guaranteed . A higher price can make it more difficult to sell the product. Thus, a change in price often must be accompanied by corresponding increases in costs, such as those for advertising, packaging, and possibly production (to enhance quality). However, even such direct changes as these may have little effect on product demand because price is often sensitive to numerous factors, such as the type of market, monopolistic elements, and product differentiation. When we increased price, we mentioned the possibility of raising the quality of the product to offset a potential loss of sales due to the price increase. For example, suppose the stitching on the denim jeans is changed to make the jeans more attractive and stronger. This change results in an increase in variable costs of $4 per pair of jeans, thus raising the variable cost per unit, c v , to $12 per pair. This change (in conjunction with our previous price change to $30) results in a new break-even volume: In general, an increase in variable costs will decrease the break-even point, all other things held constant . This new break-even volume and the change in the total cost line that occurs as a result of the variable cost change are shown in Figure 1.4. Figure 1.4. Break-even model with an increase in variable cost Next let's consider an increase in advertising expenditures to offset the potential loss in sales resulting from a price increase. An increase in advertising expenditures is an addition to fixed costs. For example, if the clothing company increases its monthly advertising budget by $3,000, then the total fixed cost, c f , becomes $13,000. Using this fixed cost, as well as the increased variable cost per unit of $12 and the increased price of $30, we compute the break-even volume as follows: In general, an increase in fixed costs will increase the break-even point, all other things held constant. This new break-even volume, representing changes in price, fixed costs, and variable costs, is illustrated in Figure 1.5. Notice that the break-even volume is now higher than the original volume of 666.7 pairs of jeans, as a result of the increased costs necessary to offset the potential loss in sales. This indicates the necessity to analyze the effect of a change in one of the break-even components on the whole break-even model. In other words, generally it is not sufficient to consider a change in one model component without considering the overall effect. Figure 1.5. Break-even model with a change in fixed cost |
EAN: 2147483647
Pages: 358