11.7 Ho and Lee model within the HJM framework
11.7 Ho and Lee model within the HJM framework
By way of an illustrative example, consider the continuous time equivalent of the Ho and Lee [ 27 ] model (studied in Chapter 10) within the above specified framework.
11.7.1 The model specifications.
Consider a model with a single Brownian motion and hence single volatility parameter ƒ 1 ( ‰ , t, T ) ‰ ƒ > 0 where ƒ is a constant. Assume Conditions 1-6 are satisfied with { f (0, T ): T ˆˆ [0, ]} the initial forward rate curve and ( ‰ , t ), t ˆˆ [0, ] themarket price of risk corresponding to the single source of randomness. From (11.32) the forward rate process with respect to the equivalent martingale measure is:
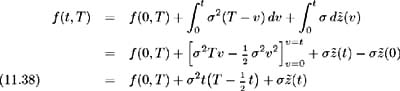
and hence the short- term interest rate process is specified as:
Since there are no restrictions placed on the evolution of the short-term or forward interest rates, there exists a positive probability of these rates being negative. To determine the bond price dynamics, substitute (11.38) into (11.2) to give:
From the definition of the forward rate (11.1), we have:
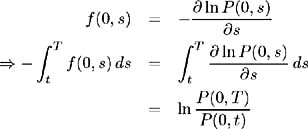
and so:
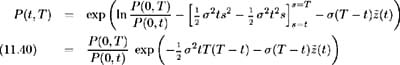
11.7.2 Pricing contingent claims.
Define the following notation:
| C ( t ) | - | time t value of a European call option on bond P ( t, T ), |
| K | - | option exercise price, |
| t * | - | option expiry date, 0 ‰ t ‰ t * ‰ T. |
At expiry of the option, its value is:
Making use of (11.36), the time t value of the contingent claim is [18] :
An analysis, similar to that used in the initial formulation of the Black- Scholes valuation formula, yields the contingent claim price to be [19] :
with
and
The above formula is a modification of the Black-Scholes option pricing formula where the required volatility is the standard deviation of instantaneous returns on the forward bond price, that is the standard deviation of returns at time t * of a bond maturing at time T . This may be determined from (11.13), the bond price process within the current framework:
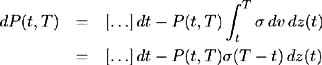
and so the standard deviation of the forward bond price ![]() is ƒ ( T ˆ’ t ) ˆ’ ƒ ( t * ˆ’ t ) = ƒ ( T ˆ’ t *).
is ƒ ( T ˆ’ t ) ˆ’ ƒ ( t * ˆ’ t ) = ƒ ( T ˆ’ t *).
[18] Here ![]() [ ·] denotes the expectation taken with respect to the equivalent martingale measure.
[ ·] denotes the expectation taken with respect to the equivalent martingale measure.
[19] Here N ( ·) is the cumulative normal distribution.
EAN: 2147483647
Pages: 132