Cryptography: Theory and Practice:Identification Schemes
 | Cryptography: Theory and Practice by Douglas Stinson CRC Press, CRC Press LLC ISBN: 0849385210 Pub Date: 03/17/95 |
| Previous | Table of Contents | Next |
9.6 Notes and References
The Schnorr Identification Scheme is from [SC91], the Okamoto Scheme was presented in [OK93], and the Guillou-Quisquater Scheme can be found in [GQ88]. Another scheme that can be proved secure under a plausible computational assumption has been given by Brickell and McCurley [BM92].
Other popular identification schemes include the Feige-Fiat-Shamir Scheme [FFS88] (see also [FS87]) and Shamir’s Permuted Kernel Scheme [SH90]. The Feige-Fiat-Shamir Scheme is proved secure using zero-knowledge techniques (see Chapter 13 for more information on zero-knowledge proofs).
The method of constructing signature schemes from identification schemes is due to Fiat and Shamir [FS87]. They also describe an identity-based version of their identification scheme.
Surveys on identification schemes have been published by Burmester, Desmedt, and Beth [BDB92] and de Waleffe and Quisquater [DWQ93].
Exercises
- 9.1 Consider the following possible identification scheme. Alice possesses a secret key n = pq, where p and q are prime and p ≡ q ≡ 3 (mod 4). The values n and ID(Alice) are signed by the TA, as usual, and stored on Alice’s certificate. When Alice wants to identify herself to Bob, say, Bob will present Alice with a random quadratic residue modulo n, say x. Then Alice will compute a square root y of x and give it to Bob. Bob then verifies that y2 ≡ x (mod n). Explain why this scheme is insecure.
- 9.2 Suppose Alice is using the Schnorr Scheme where q = 1201, p = 122503, t = 10 and α = 11538.
- (a) Verify that α has order q in
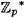 .
.- (b) Suppose that Alice’s secret exponent is a = 357. Compute v.
- (c) Suppose that k = 868. Compute γ.
- (d) Suppose that Bob issues the challenge r = 501. Compute Alice’s response y.
- (e) Perform Bob’s calculations to verify y.
- (b) Suppose that Alice’s secret exponent is a = 357. Compute v.
- 9.3 Suppose that Alice uses the Schnorr Scheme with p, q, t and α as in Exercise 9.2. Now suppose that v = 51131, and Olga has learned that
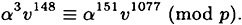
Show how Olga can compute Alice’s secret exponent a.
- 9.4 Suppose that Alice is using the Okamoto Scheme with q = 1201, p = 122503, t = 10, α1 = 60497 and α2 = 17163.
- (a) Suppose that Alice’s secret exponents are a1 = 432 and a2 = 423. Compute v.
- (b) Suppose that k1 = 389 and k2 = 191. Compute γ.
- (c) Suppose that Bob issues the challenge r = 21. Compute Alice’s response, y1 and y2.
- (d) Perform Bob’s calculations to verify y1 and y2.
- (b) Suppose that k1 = 389 and k2 = 191. Compute γ.
- 9.5 Suppose that Alice uses the Okamoto Scheme with p, q, t, α1, and α2 as in Exercise 9.4. Suppose also that v = 119504.
- (a) Verify that
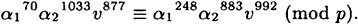
- (b) Use this information to compute b1 and b2 such that
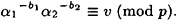
- (c) Now suppose that Alice reveals that a1 = 484 and a2 = 935. Show how Alice and Olga together will compute
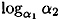 .
. - (b) Use this information to compute b1 and b2 such that
- 9.6 Suppose that Alice is using the Guillou-Quisquater Scheme with p = 503, q = 379, and b = 509.
- (a) Suppose that Alice’s secret u = 155863. Compute v.
- (b) Suppose that k = 123845. Compute γ.
- (c) Suppose that Bob issues the challenge r = 487. Compute Alice’s response, y.
- (d) Perform Bob’s calculations to verify y.
- (b) Suppose that k = 123845. Compute γ.
- 9.7 Suppose that Alice is using the Guillou-Quisquater Scheme with n = 199543, b = 523 and v = 146152. Suppose that Olga has discovered that
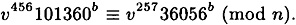
Show how Olga can compute u.
- 9.2 Suppose Alice is using the Schnorr Scheme where q = 1201, p = 122503, t = 10 and α = 11538.
| Previous | Table of Contents | Next |
Copyright © CRC Press LLC
EAN: 2147483647
Pages: 133