Cryptography: Theory and Practice:Classical Cryptography
 | Cryptography: Theory and Practice by Douglas Stinson CRC Press, CRC Press LLC ISBN: 0849385210 Pub Date: 03/17/95 |
| Previous | Table of Contents | Next |
DEFINITION 1.6 A Stream Cipher is a tuple  , where the following conditions are satisfied:
, where the following conditions are satisfied:
- 1.
 is a finite set of possible plaintexts
is a finite set of possible plaintexts - 2.
 is a finite set of possible ciphertexts
is a finite set of possible ciphertexts - 3.
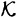 , the keyspace, is a finite set of possible keys
, the keyspace, is a finite set of possible keys - 4.
 is a finite set called the keystream alphabet
is a finite set called the keystream alphabet - 5.
 is the keystream generator. For i ≥ 1,
is the keystream generator. For i ≥ 1, 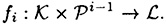
- 6. For each
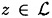 , there is an encryption rule
, there is an encryption rule 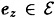 and a corresponding decryption rule
and a corresponding decryption rule 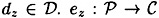 and
and 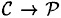 are functions such that dz(ez(x)) = x for every plaintext
are functions such that dz(ez(x)) = x for every plaintext 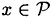 .
. - 2.
We can think of a block cipher as a special case of a stream cipher where the keystream is constant: zi = K for all i ≥ 1.
Here are some special types of stream ciphers together with illustrative examples. A stream cipher is synchronous if the keystream is independent of the plaintext string, that is, if the keystream is generated as a function only of the key K. In this situation, we think of K as a “seed” that is expanded into a keystream z1z2 . . ..
A stream cipher is periodic with period d if Zi+d = zi for all integers i ≥ 1. The Vigenere Cipher with keyword length m can be thought of as a periodic stream cipher with period m. In this case, the key is K = (k1, . . . , km). K itself provides the first m elements of the keystream: zi = ki, 1 ≤ i ≤ m. Then the keystream just repeats itself from that point on. Observe that in this stream cipher setting for the Vigenere Cipher, the encryption and decryption functions are identical to those used in the Shift Cipher: ez(x) = x + z and dz (y) = y - z.
Stream ciphers are often described in terms of binary alphabets, i.e.,  . In this situation, the encryption and decryption operation are just addition modulo 2:
. In this situation, the encryption and decryption operation are just addition modulo 2:
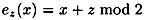
and
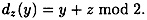
If we think of “0” as representing the boolean value “false” and “1” as representing “true,” then addition modulo 2 corresponds to the exclusive-or operation. Hence, encryption (and decryption) can be implemented very efficiently in hardware.
Let’s look at another method of generating a (synchronous) keystream. Suppose we start with (k1, . . . , km) and let zi = ki, 1 ≤ i ≤ m (as before), but we now generate the keystream using a linear recurrence relation of degree m:

where c0, . . . , 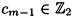 are predetermined constants.
are predetermined constants.
REMARK This recurrence is said to have degree m since each term depends on the previous m terms. It is linear because zi+m is a linear function of previous terms. Note that we can take c0 = 1 without loss of generality, for otherwise the recurrence will be of degree m - 1.
Here, the key K consists of the 2m values k1, . . . , km, c0, . . . , cm-1. If
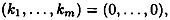
then the keystream consists entirely of 0’s. Of course, this should be avoided, as the ciphertext will then be identical to the plaintext. However, if the constants c0, . . . , cm-1 are chosen in a suitable way, then any other initialization vector (k1, . . . , km) will give rise to a periodic keystream having period 2m - 1. So a “short” key can give rise to a keystream having a very long period. This is certainly a desirable property: we will see in a later section how the Vigenere Cipher can be cryptanalyzed by exploiting the fact that the keystream has short period.
Here is an example to illustrate.
Example 1.7
Suppose m = 4 and the keystream is generated using the rule

(i ≥ 1). If the keystream is initialized with any vector other than (0, 0, 0, 0), then we obtain a keystream of period 15. For example, starting with (1, 0, 0, 0), the keystream is
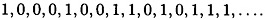
Any other non-zero initialization vector will give rise to a cyclic permutation of the same keystream.
Another appealing aspect of this method of keystream generation is that the keystream can be produced efficiently in hardware using a linear feedback shift register, or LFSR. We would use a shift register with m stages. The vector (k1, . . . , km) would be used to initialize the shift register. At each time unit, the following operations would be performed concurrently:
- 1. k1 would be tapped as the next keystream bit
- 2. k2, . . . , km would each be shifted one stage to the left
- 3. the “new” value of km would be computed to be
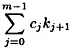
(this is the “linear feedback”).
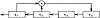
Figure 1.8 A Linear Feedback Shift Register
Figure 1.9 Autokey Cipher - 2. k2, . . . , km would each be shifted one stage to the left
Observe that the linear feedback is carried out by tapping certain stages of the register (as specified by the constants cj having the value “1”) and computing a sum modulo 2 (which is an exclusive-or). This is illustrated in Figure 1.8, where we depict the LFSR that will generate the keystream of Example 1.7.
An example of a non-synchronous stream cipher that is known as the Autokey Cipher is given in Figure 1.9. It is apparently due to Vigenere.
The reason for the terminology “autokey” is that the plaintext is used as the key (aside from the initial “priming key” K). Here is an example to illustrate:
| Previous | Table of Contents | Next |
Copyright © CRC Press LLC
EAN: 2147483647
Pages: 133