POISSON DISTRIBUTION: LIMIT OF BINOMIAL DISTRIBUTION FOR RARE OCCURRENCE

Rare successes: Probability p extremely small but sample size n extremely large, such that binomial mean = np = a is finite. Since p is so small, we can expect that x success will also be small compared to sample size n. The Poisson distribution is also used to compute the probability of the number of "Poisson events" during a given time interval or within a specified region of space.

We already have defined the binomial distribution as:

For the Poisson distribution, however, we:

1. Reduce the permutation factor, since x << n.

   

2. Combine factors of like powers.

   

3. Note that because p « 1 and x is not large, we can approximate (1 - p) ^x = 1.

4. Having mean np = a we can rewrite n = a/p so

   

5. Limit as p ’ 0 yields exponential

   

6. The result is the Poisson distribution (one parameter: a).

   

   1. In reliability, the parameter a = t.

   2. is the mean number of events per unit time.

COMPARISON OF BINOMIAL AND POISSON

The probability density function (pdf) for the binomial distribution is:

B (Xi = x;n, p) = [n!/X!(n - x)!] p ^x q ^(n-x)

• Mean: ¼ = np = a

• Variance: ƒ ² = npq = aq

• Two Parameters: n and p

  • or

  • a(= np) and q = (1- p)

On the other hand, the probability function for the Poison distribution is:

where a = n p and q = (1 - p) approx. 1.

• Mean: ¼ = a

• Variance: ƒ ² = a

• One parameter: a( = np)

Example 5

A compressor manufacturer has a record of 50 defects per 1000 produced, which corresponds to a defect percentage of 5%. Since the probability of successfully observing a defect is small (p = 0.05), then we can assume a Poisson distribution.

Determine probability of observing defects in batch of n = 10:

Poisson parameter: a = np = 10(0.05) = 0.5

Probability of exactly x = 0 failures:

Probability of exactly x = 1 failure:

Probability of exactly x = 2 failures:

Probability of exactly x = 3 failures:

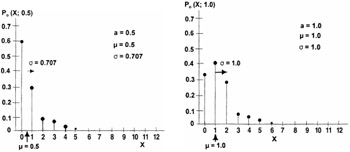
Figure 16.32 shows the Poisson distribution for each of the failures.

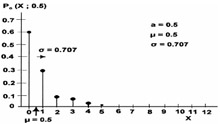
Figure 16.32: Poisson distribution for the four failures.

Special comments:

1. The mean is equal to the parameter a; as a result, the smaller the "a's," the more skewed the probability density function (pdf) is to the left.

   

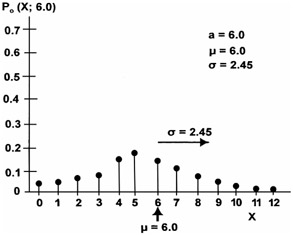
2. The standard deviation is equal to the square root of "a"; hence, increasing the value of "a" also increases the standard deviation.

3. The larger the value of "a," the more the Poisson distribution approaches the normal distribution.