CENTRAL LIMIT THEOREM (CLT) - MEAN OF MEANS IS NORMAL (FIGURE 16.28)

CENTRAL LIMIT THEOREM (CLT) ” MEAN OF MEANS IS NORMAL (FIGURE 16.28)

• Statistical inference based on normal distribution.

• Estimation techniques based on normal distribution.

• Real data distribution may not be normal.

• Work with mean of sample clusters, not individual values X _i .

• CLT uses normal distribution to infer population parameter: Mean ¼ and Variance ƒ ²

Mathematically the mean of means may be represented by

Whereas the variance of the means is represented as:

where n = number of individual samples in a subject or cluster. If there are clusters, the M = total number of clusters, nM = N = total number of individual samples.

COMMENTS ON THE SND

For a cluster of n samples, we can use SND to determine:

1. The probabilities of the sample average, 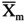or,

2. The required number of samples, n, in a cluster such that is observed mean X _m is within a specified range around the true population mean ¼ .

   • The cluster size n can be quite small, and the histogram of cluster mean values, X _m , will rapidly converge to a normal distribution regardless of the underlying population.

   • The Central Limit Theorem applies to any population distribution, including the discrete and continuous distributions as well as bimodal distributions.

   • When discrete sampling is involved, the distribution of averages (i.e., the mean of clusters) must be used.

   • The variance of the means is a measure of the spread of clusters means about the true mean.

   • Variance gets smaller as n increases ; the smaller the number of samples in a cluster the larger the variance of the means.