UNIFORM DISTRIBUTION
If we consider each die as an independent random variable, then a uniform probability distribution will be the result and will take the shape shown in Figure 16.8.
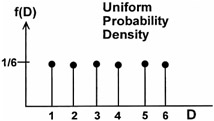
Figure 16.8: Uniform probability density for a die.
With mean value of single die:
Variance about mean:
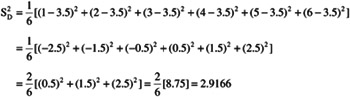
Standard deviation: S D = 1.708
The uniform distribution may be represented in general mathematical notation along with the constraints as:

and the shape looks like Figure 16.9.
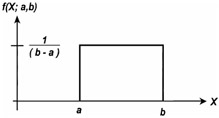
Figure 16.9: A generic uniform distribution.
When checking for the probability density function of a uniform distribution one should check the following two properties:
-
Positive: f {X; a,b) ‰ O
-
Unit area:

| Note | Height of p.d.f. is equal to the reciprocal of the base. Figure 16.10 shows the comparison of the uniform distribution and the cumulative density function.  Figure 16.10: A comparison of the uniform distribution and its C.D.F. |
The mathematical notation of the c.d.f. with the constraints is:
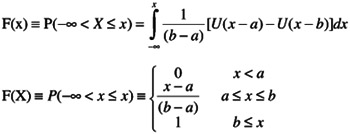
Mean:
Variance:
The reader will notice that in the uniform distribution, (1) median = mean, and (2) there is no mode.
| |
Sound level in a room is found to be uniformly distributed between 80 and 95 dBA. Occupational Safety and Health Administration (OSHA) regulations set a maximum safe level of 90 dBA for an 8- hour workday . See Figure 16.11.
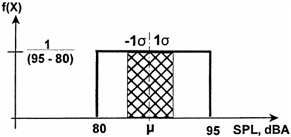
Figure 16.11: The sound level in a room.
Find:
-
The probability density function, f(x) for this noise
-
The probability of exceeding the 90 dBA standard
-
The mean and standard deviation
-
The level range within ± 1 ƒ of the mean
-
The probability of being in this ± 1 ƒ about the mean
Solutions:
-
f(X) = 1/15; 80 ‰ x ‰ 95
-
Probability of exceeding 90 dBA:
P(> 90) = 1 - P(x ‰ 90) = 1 - F(x = 90)
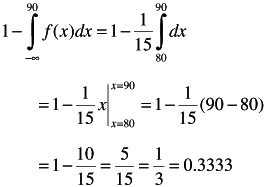
-
Mean:
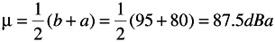
Standard Deviation:
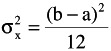
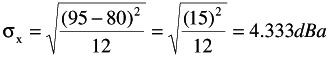
-
One-sigma range about mean: ( ¼ - 1 ƒ ) ‰ x ‰ ( ¼ + 1 ƒ )
83.2 ‰ x ‰ 91.8
-
Probability of SPL being in this one-sigma range
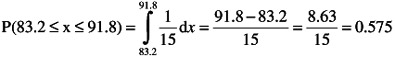
| |
EAN: 2147483647
Pages: 252