DISCRETE CUMULATIVE DISTRIBUTION FUNCTION

Probability that value of the random variables X _k will be less than or equal to a specified value X _m .

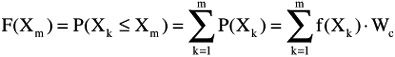
where the capital letter F is used for cumulative distribution. If sample space is a finite number K of random variables:

x = {X ₁ , X ₂ , X ₃ , ..., X _k , ..., X _m , ..., X _K }

where we assume an ascending order: X _k-1 < X _k < X _k+1 .

For example, if m = 2:

F (X 2 )	=	f (X 1 ) · W c + f (X 2 ) · W c
	=	P (X 1 ) + P (X 2 )
	=	P (X k ‰ X 2 )

Upper bound: m = K

F(X _K ) = P(X _k ‰ X _K ) = 1

RANDOM EXPERIMENT

Two tosses of a coin.

Random Variable X _k defined as number of heads. (Grouped data X _k has a cell width of unity W _c = 1.)

R.V.X k Prob. Fn. f(X k ) Cumulative Prob. F(X k )
X k < 0	P(X < X 1 ) = 0
X 1 = 0	f(X 1 ) = 1/4	F(X 1 ) = P(x ‰ X 1 ) = 1/4
X 2 = 1	f(X 2 ) = 1/2	F(X 2 ) = P(x ‰ X 2 )
		= P(X 1 ) + P(X 2 )
		= 1/4 + 1/2 = 3/4
X 3 = 2	f(X 3 ) = 1/4	F(X 3 ) = P(x ‰ X 3 )
		= P(X 1 ) + P(X 2 ) + P(X 3 )
		= 1/4 + 1/2 + 1/4 = 1

Figure 16.3 shows the cumulative distribution of two tosses of a coin.

Figure 16.3: Cumulative distribution of two tosses of a coin.

RANDOM EXPERIMENT

Toss a pair of fair dice.

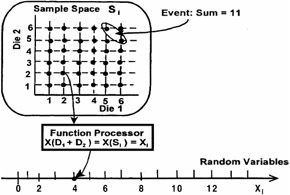
Individual Sample S _i : Defined as sum of face values on pair of six-sided dice.

S _i = D ₁ + D ₂

Total sample space size : N = 6 — 6 = 36 possible outcomes

Random Variable X _k : Is cell equal to a specific value of S _i

X _k= {S _i } = {D ₁ + D ₂ }

It is quite common in engineering to have numerical value samples.

Total number of Random Variables cells : M = 11

Range of RV: [X ₁ = 2 ‰ X _k ‰ 12 = X ₁₁ ]

Other possible processes (and distributions) could include:

1. Product: S _i = D ₁ · D ₂

2. Magnitude of difference: S _i = D ₁ - D ₂

3. Ratio: S _i = D ₁ /D ₂

Random Variable: (X _k = {S _i } = {D ₁ + D ₂ })

X (Die 1 + Die 2) = X(Sum) = Sum = X _(Sum-1)

Example outcome:

X ([Die 1 = 1] + [Die 2 = 2]) = X(1 + 2) = 3 = X ₂

Consider an event A: Set of all RVs equal to 3

{X ₂ } = {[1 + 2], [2 + 1]} = {3, 3}

Sample size of event A is therefore m = 2

Probability Density: particular event {X ₂ }

f(X ₂ ) = P(X ₂ ) = m/N

or

f(3) = P(3) = 2/36

Cumulative distribution: for random variable X ₂ = 3

F(X ₂ ) = f(X ₁ ) + f(X ₂ )

or

F(3)	=	f(2) + f(3)
	=	1/36 + 2/36 = 3/36

S _i = D ₁ + D ₂ = Sum of numbers appearing on face cell: X _k = {S _i } = {D ₁ + D ₂ }

The probabilities associated with each cell are shown in Table 16.1

Figure 16.4 shows the probability density function and Figure 16.5 shows the cumulative probability function.

Figure 16.4: Probability density function.

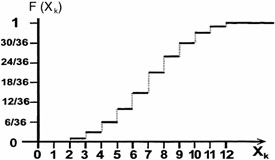
Figure 16.5: Cumulative probability function.

Table 16.1: Probability Density and Distribution of a Pair of Fair Dice

R.V. X k	No. Outcomes with Value X k	f (X k )	F (X k )
2	1	1/36	1/36
3	2	2/36	3/36
4	3	3/36	6/36
5	4	4/36	10/36
6	5	5/36	15/36
7	6	6/36	21/36
8	5	5/36	26/36
9	4	4/36	30/36
10	3	3/36	33/36
11	2	2/36	35/36
12	1	1/36	36/36
	Sum = 36	36/36