Chapter 15: Permutations and Combinations
This chapter discusses elementary probability calculations and the "counting rules" that underlie the development of several distributions such as the binomial, hypergeometric, and Poisson. Perhaps one of the most essential concepts in statistical theory as applied in the field of quality is the issue of combinations. This chapter presents a cursory overview of this mathematical expansion and its use. If you are interested in pursuing the subject in more detail, please consult some basic statistics or probability books.
RULES
We begin by defining the counting rules:
-
Rule 1: If any one of K mutually exclusive and exhaustive events can occur on each of N trials, then there are K N different sequences that may result from a set of trials.
-
Rule 2: If K 1 , ..., K N are the numbers of distinct events that can occur on trials 1, ..., N in a series, then the number of different sequences of N events that can occur is (K 1 )(K 2 ) ... (K N ).
-
Rule 3: The number of different ways that N distinct things may be arranged in order is N! = (1)(2)(3) ... (N - 1)(N), where 0! = 1. An arrangement in order is called permutation, so that the total number of permutations of N objects is N! The symbol N! is called "N factorial."
A more generic notation is:
n! ‰ (n) (n - 1) (n - 2)... (n - (n - 2)) (2) (1) = n(n - 1)!
where 1 ! = 1 and 0! ‰ 1 but (-n)! is undefined .
-
Stirling's approximation to n!: For large values of n it is difficult to determine the value of n! Therefore, we can use the approximation:
n! ‰ƒ
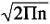 n n e -n
n n e -n Note Most computers, including hand-held calculators , have a factorial key n! which reduces the need to apply Stirling's approximation.
-
Rule 4: The number of ways of selecting and arranging r objects from among N distinct objects is N!/(N - r)!
-
Rule 5: The total number of ways of selecting r distinct combinations of N objects, irrespective of order, is N!/r!(N - r) =
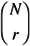
EAN: 2147483647
Pages: 252
- Key #1: Delight Your Customers with Speed and Quality
- Key #2: Improve Your Processes
- Key #4: Base Decisions on Data and Facts
- Making Improvements That Last: An Illustrated Guide to DMAIC and the Lean Six Sigma Toolkit
- The Experience of Making Improvements: What Its Like to Work on Lean Six Sigma Projects