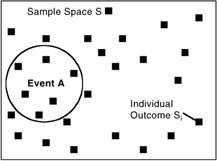
SAMPLE SPACE: S

1. Equivalent to universal space U

   • Related to a random experiment

     • Uncertainty of results or outcomes

   • Consists of all possible outcomes or samples

   • Each output is a simple or elementary event, S _i

   • Discrete, e.g., selecting a card or coin tosses

   • Continuous, e.g., diameter or weight of rods

   • Finite or infinite

   

2. Events of sample space: A

   • Simple or elementary event is one (individual) outcome of sample space, S _i .

     

   • An event A is a subset or grouping of simple events; e.g., event A of n simple events: A = {S ₁ , ..., S _n }

   • Elements of event A are samples with defined characteristics; e.g., the odd numbers tossed on dice.

If the outcome of an experiment S _i is an element of A, then "the event A has occurred."

EXAMPLES OF SETS

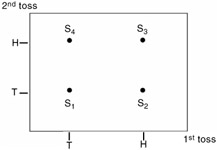
Given: Random experiment in a twice-tossed coin.

1. Find the sample space S of the four possible outcomes:

   Simple events: S ₁ = TT, S ₂ = HT, S ₃ = HH, S ₄ = TH

   Sample space: S = (S ₁ , S ₂ , S ₃ , S ₄ )

   

2. Find the subset or event A defined as when: At least one head occurs.

   Event A = (HT, HH, TH) = (S ₂ , S ₃ , S ₄ )

   

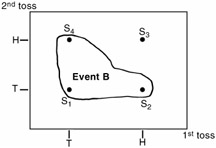
3. Find the subset or event B defined as when: At least one tail occurs.

   Event B = (TT, HT, TH) = (S ₁ , S ₂ , S ₄ )

   

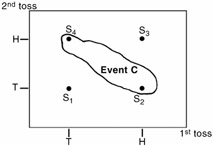
4. Find the subset or event C defined as when: At least one head (event A) AND one tail (event B) occur.

   Event C = (HT, TH) = (S ₂ , S ₄ )

   "AND" in set theory is an "intersection," meaning "both A and B."

   C	‰	A ‹‚ B
   	‰	(S 2 , S 4 )

   

5. Find the subset or event D defined as when: The first toss is a head.

   Event D = (HT, HH) = (S ₂ , S ₃ )

   

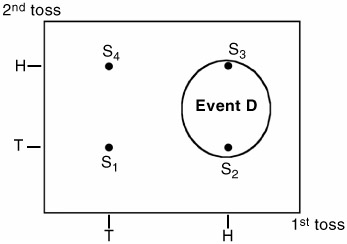
6. Find the subset or event E defined as when: At least one head (event A) OR at least one tail (event B) occurs.

   Event E = (TT, HT, HH, TH) = (S ₁ , S ₂ , S ₃ , S ₄ )

   "OR" in set theory is "union," meaning "either A or B or both."

   E ‰ A ‹ƒ B = (S ₁ , S ₂ , S ₃ , S ₄ ) = S

7. Find the event F that CANNOT occur assuming the event A does occur. Event A is defined as when at least one head occurs.

   Event A = (HT, HH, TH) = (S ₂ , S ₃ , S ₄ )

   Event F is the event "not A."

   Event F = (TT) = (S ₁ )

   Event A and event F are " mutually exclusive" or " disjoint " in set theory.

   A ‹‚ F = =A ‹‚ A'

   Hence the event

   F = A' = (S ₁ ) = (TT)