DEMING S FUNNEL EXPERIMENT AND TAMPERING | Six Sigma and Beyond: Statistical Process Control, Volume IV

DEMING'S FUNNEL EXPERIMENT AND TAMPERING

In the quest for reduced variability, it is tempting to make frequent small adjustments to a system. However, if the system is already in control, these adjustments can actually make a system worse . Deming called this "tampering" and often demonstrated it in his seminars with the following funnel experiment.

To illustrate the idea, suppose that we are in the business of drilling a tiny hole in the exact center of a square piece of wood. In the past, the holes we have drilled have averaged being in the center of the wood, with both the x and y coordinates having a standard deviation of 0.1 inch. Also, the drilling process has been in control. Specifically, the deviations from the center of the square (measured in each of the x and y coordinates) follow a normal distribution, with a mean of 0 and a standard deviation of 0.1 inch. This means, for example, that 68% of the holes have their x coordinate within 0.1 inch of the center; 95% of the holes have their x coordinate within 0.2 inch of the center; and 99.7% of the holes have their x coordinate within 0.3 inch of the center. This describes the inherent variability in the drilling process. Without changing the process by which holes are drilled, we must live with this amount of variation.

Now suppose that we drill a hole and its x and y coordinates are x = 0.1 and y = 0 [where the center of the square has coordinates (0,0)]. A natural reaction is to reduce (if possible) the x setting of the drill by 0.1 inch to correct for the fact that the x coordinate was too high. Then if the next hole has coordinates of x = -0.2 and y = 0.1, we might try to increase the x coordinate by 0.2 inch and decrease the y coordinate by 0.1 inch. Deming's funnel experiment shows that this method of continually readjusting an in-control process tampering will actually increase the variability of the distance of the holes from the target. That is, tampering will generally make the process worse!

To illustrate the effects of tampering, Deming placed a funnel above a target on the floor and dropped small balls through the funnel in an attempt to hit the target. As he demonstrated, many balls did not hit the target. His goal, therefore, was to make the balls fall as close to the target as possible. Deming proposed four rules for adjusting the position of the funnel.

RULES FOR FUNNEL EXPERIMENT

Never move the funnel.
After each ball is dropped, move the funnel relative to its previous position to compensate for any error. To illustrate, suppose the funnel begins directly over the target, at coordinates (0,0). If the ball lands at (0.5, 0.1) on the first drop, we compensate by repositioning the funnel at (-0.5, -0.1). If the second drop has coordinates (1, -2), we now reposition the funnel at (-0.5 -1, -0.1 - (-2)) = (-1.5, 1.9).
Move the funnel relative to its original position at (0,0) to compensate for any error. If the ball lands at (0.5, 0.1) on the first drop, we compensate by repositioning the funnel at (-0.5, -1). If the second drop has coordinates (1, -2), we now reposition the funnel at (0 - 1, 0 - [-2]) = (-1, 2).
Always reposition the funnel directly over the last drop. Thus if the first ball lands at (0.5, 1), we reposition the funnel to (0.5, 1). If the second drop has coordinates of (1, 2), we reposition the funnel to (1, 2). This rule might be followed, for example, by an automobile manufacturer's painting department. With each new batch of paint, they attempt to match the color of the previous batch, whether or not the previous color was "correct."

To see how these rules work, we run a simulation in Excel. We assume that the x coordinate on each drop is normally distributed with a mean equal to the x coordinate of the funnel position and a standard deviation of 1. A similar statement holds for the y coordinate. Also, we assume that the x and y coordinates are selected independently of one another. These assumptions describe the inherent variability in the process of dropping the balls.

To run the simulation, we simulate 50 consecutive drops of the ball and then use a data table to replicate the distance from the 50th drop to the target 100 times. A good rule should have a small average distance, and the standard deviation of the distances (across the replications) should also be small.

On the basis of the simulation, the following statistics are generated based on each rule (see Table 6.1):

Table 6.1: Distance for the Simulated Drops
	Rule 1	Rule 2	Rule 3	Rule 4
Average	1.28	1.87	9.11	9.58
Standard deviation	0.65	0.88	4.98	4.99
Maximum	3.60	4.36	24.96	25.91

It helps to introduce some notation. Let P _x,t and P _y,t be the x and y coordinates of the position of the funnel just before drop t, where P _x _, ₁ and P _y, ₁ , the coordinates of the initial position, are both set to 0 for all of the rules. Also, let X _t and Y _t be the coordinates at which drop t actually falls . Our assumptions imply that X _t and Y _t are normally distributed, with means P _x,t and and P _y,t . The four rules determine the coordinates of the next funnel position, P _x,t ₊₁ and P _y,t+ ₁ , as in Table 6.2.

Table 6.2: The Coordinates for the Funnel Experiment
P _x,t ₊₁ = P _x,t	P _y,t+ ₁ = P _y,t	Rule 1
P _x,t ₊₁ = P _x,t - X _t	P _y,t+ ₁ = P _y.t - Y _t	Rule 2
P _x,t+ ₁ = 0 - X _t = - X _t	P _y,t+ ₁ = 0 - Y _t = -Y _t	Rule 3
P _x,t+ ₁ = X _t	P _y,t+ ₁ = Y _t	Rule 4

These equations allow us to simulate 50 consecutive drops for any of the four rules very easily in Excel. After implementing each of the four rules for 50 drops, we apply the simulation to replicate the distance from the 50th drop to the target for each rule 100 times. (Each distance is the square root of the sum of squares of the coordinates of the 50th drop.) The average, standard deviation, and maximum of the 100 distances appear in Table 6.1. Because we want these distances to be small, we see that Rule 1 is performing best, with Rule 2 following fairly close behind and Rules 3 and 4 performing terribly.

This behavior is reinforced by the histograms of the 100 replicated distances for each rule in Figures 6.8 “6.11. (They are all shown on the same scale to facilitate comparisons.) As we see, most of the distances for Rule 1 are within 2 units of the target, and most of the distances for Rule 2 are within 3 units of the target, but most of the distances for Rules 3 and 4 are more than 9 units from the target. As Deming predicted , tampering with an in-control system never helps, and it can have very negative consequences.

We conclude this discussion of the funnel experiment by noting that the system obtained by using Rule 1, the leave-it-alone rule, is not necessarily a good system. It may indeed require improvement. The point, though, is that continual tampering with this system will not produce the required improvement; it will only tend to make things worse. The only way to make a lasting improvement to the system is for management to change it frequently. Workers performing their daily routine do not typically have the knowledge or authority to make such a fundamental change. This must come from the management.

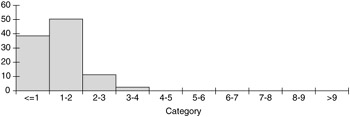
Figure 6.8: Histogram of distances for Rule 1.

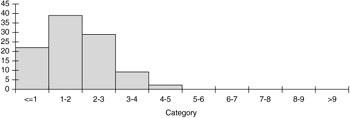
Figure 6.9: Histogram of distances for Rule 2.

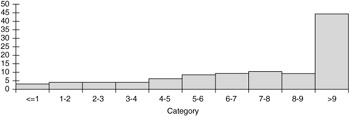
Figure 6.10: Histogram of distances for Rule 3.

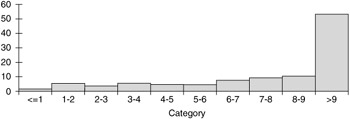
Figure 6.11: Histogram of distances for Rule 4.