WEIBULL DISTRIBUTION

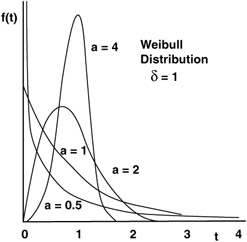
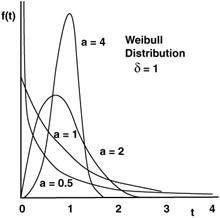
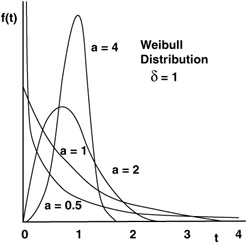
One of the more popular models for time-to-failure (TTF), Weibull distributions take many shapes and are typically identified as in the following illustration.

Weibull probability density function (pdf)

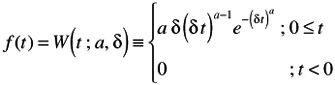
Cumulative distribution

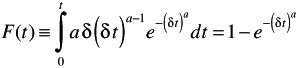
Two parameters:

Shape parameter:	a	(changes shape not scale)
Scale parameter:		(changes scale not shape)

Some authors define = 1/ · and a = ²

In a typical Weibull distribution shown below, there are some general characteristics

• Mean:

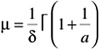
• Variance:

• 1/ also referred to as "characteristic life" or "time constant," the life or time at which 63.2% of population has failed.

• If a = 1, the Weibull reduces to the exponential distribution.

• If a = 2, the Weibull reduces to the Rayliegh distribution.

• If a ‰ˆ 3.5, the Weibull approximates the normal distribution.

• For a < 1, reliability function decays less rapidly .

• For a > 1, reliability function decays more rapidly.

• A useful model for the failure time (or length of life) distributions of produces and processes.

• Does not assume that the failure rate, , is a constant as do the Exponential and Gamma distributions.

• Has the advantage that the distribution parameters can be adjusted to fit many situations; because of this adaptability it is widely used in reliability engineering.

• The cumulative distribution has closed form expression that can be used to compute areas under the Weibull curve.

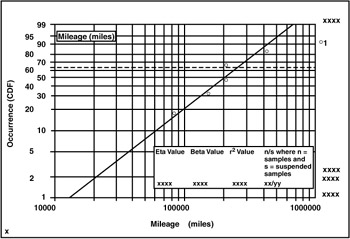
• Estimates of the two parameters, and a, can be obtained when ranked sample data are plotted on scale adjusted cumulative percentile (See Probability Plots).

Note  

Characteristic life t = 1/

corresponds to the 63.2%

• Weibull reliability or survival function:

  

• Weibull failure distribution: (same as cumulative distribution)

  

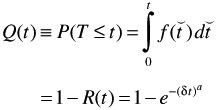
• Weibull hazard rate function:

  

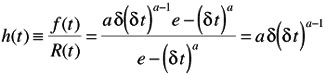
• The shape parameter a, can be used to adjust the shape of the Weibull distribution to allow it to model a great many life (time) related distributions found in engineering.

  

THREE-PARAMETER WEIBULL DISTRIBUTION

If failures do not have the possibility of starting at t = 0, but only after a finite time t _O , a time-shift variable can be used to redefine the Weibull reliability function:

R ( t ) =

where the time t _O is called the failure free time or minimum life.