Chapter 55: An Introduction to Random Variables | MicrosoftВ® Office ExcelВ® 2007: Data Analysis and Business Modeling (Bpg -- Other)

Overview

What is a random variable?
What is a discrete random variable?
What are the mean, variance, and standard deviation of a random variable?
What is a continuous random variable?
What is a probability density function?
What are independent random variables?

In today’s world, the only thing that’s certain is that we face a great deal of uncertainty. In the next nine chapters, I’ll give you some powerful techniques that you can use to incorporate uncertainty in business models. The key building block in modeling uncertainty is understanding how to use random variables.

What is a random variable?
Any situation whose outcome is uncertain is called an experiment. The value of a random variable is based on the (uncertain) outcome of an experiment. For example, tossing a pair of dice is an experiment, and a random variable might be defined as the sum of the values shown on each die. In this case, the random variable could assume any of the values 2, 3, and so on up to 12. As another example, consider the experiment of selling a new video game console, for which a random variable might be defined as the market share for this new product.
What is a discrete random variable?
A random variable is discrete if it can assume a finite number of possible values. Here are some examples of discrete random variables:
- Number of potential competitors for your product
- Number of aces drawn in a five-card poker hand
- Number of car accidents you have (hopefully zero!) in a year
- Number of dots showing on a die
- Number of free throws out of 12 that Steve Nash makes during a basketball game
What are the mean, variance, and standard deviation of a random variable?
In Chapter 37, “Summarizing Data with Descriptive Statistics,” I discussed the mean, variance, and standard deviation for a data set. In essence, the mean of a random variable (often denoted by μ) is the average value of the random variable we would expect if we performed an experiment many times. The mean of a random variable is often referred to as the random variable’s expected value. The variance of a random variable (often denoted by σ²) is the average value of the squared deviation from the mean of a random variable that we would expect if we performed our experiment many times. The standard deviation of a random variable (often denoted by σ) is simply the square root of its variance. As with data sets, the mean of a random variable is a summary measure for a typical value of the random variable, whereas the variance and standard deviation measure the spread of the random variable about its mean.
As an example of how to compute the mean, variance, and standard deviation of a random variable, suppose we believe that the return on the stock market during the next year is governed by the following probabilities:

Open table as spreadsheet

Probability

Market return

.40

+20 percent

.30

0 percent

.30

-20 percent

Probability	Market return
.40	+20 percent
.30	0 percent
.30	-20 percent

Hand calculations show the following:

 μ=.40*(.20)+.30*(.00)+.30*(−.20)=.02 or 2 percent σ²=.4*(.20−.02)²+.30*(.0−.02)²+.30*(−.20−.02)²=.0276

Then σ=.166 or 16.6 percent.
In the file Meanvariance.xlsx (shown in Figure 55-1), I’ve verified these computations.

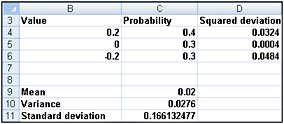
Figure 55-1: Computing the mean, standard deviation, and variance of a random variable
I computed the mean of our market return in cell C9 with the formula =SUMPRODUCT(B4:B6,C4:C6). This formula multiplies each value of the random variable by its probability and sums up the products.
To compute the variance of our market return, I determined the squared deviation of each value of the random variable from its mean by copying from D4 to D5:D6 the formula =(B4–$C$9)^2. Then, in cell C10, I computed the variance of the market return as the average squared deviation from the mean with the formula =SUMPRODUCT (C4:C6,D4:D6). Finally, I computed the standard deviation of the market return in cell C11 with the formula =SQRT(C10).
What is a continuous random variable?
A continuous random variable is a random variable that can assume a very large number or, to all intents and purposes, an infinite number of values. Here are some examples of continuous random variables:
- Price of Microsoft stock one year from now
- Market share for a new product
- Market size for a new product
- Cost of developing a new product
- Newborn baby’s weight
- Person’s IQ
- Dirk Nowitzki’s three-point shooting percentage during next season
What is a probability density function?
A discrete random variable can be specified by a list of values and the probability of occurrence for each value of the random variable. Because a continuous random variable can assume an infinite number of values, we can’t list the probability of occurrence for each value of a continuous random variable. A continuous random variable is completely described by its probability density function. For example, the probability density function for a randomly chosen person’s IQ is shown in Figure 55-2.

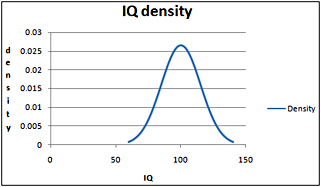
Figure 55-2: Probability density function for IQs
A probability density function (pdf) has the following properties:
- The value of the pdf is always greater than or equal to 0.
- The area under the pdf equals 1.
- The height of the density function for a value x of a random variable is proportional to the likelihood that the random variable assumes a value near x. For example, the height of the density for an IQ of 83 is roughly half the height of the density for an IQ of 100. This tells us that IQs near 83 are approximately half as likely as IQs around 100. Also, because the density peaks at 100, IQs around 100 are most likely.
- The probability that a continuous random variable assumes a range of values equals the corresponding area under the density function. For example, the fraction of people having IQs from 80 through 100 is simply the area under the density from 80 through 100.
What are independent random variables?
A set of random variables are independent if knowledge of the value of any of their subsets tells you nothing about the values of the other random variables. For example, the number of games won by the Indiana University football team during a year is independent of the percentage return on Microsoft during the same year. Knowing that Indiana did very well would not change your view of how Microsoft stock did during the year.
On the other hand, the returns on Microsoft stock and Intel stock are not independent. If we are told that Microsoft stock had a high return in one year, in all likelihood, computer sales were high, which tells us that Intel probably had a good year as well.