Methods As Building Blocks: Encapsulating Your Helper Methods with the private keyword

---

Methods As Building Blocks: Encapsulating Your Helper Methods with the private keyword.

We can expect the internal parts of each class in a program to be less complex than the overall program, but the programmer is still often confronted with individual classes of relatively high complexity. Fortunately, it is possible to reduce this complexity by dividing its functionality into methods. Let's look at an example.

Notice that this discussion is relevant to step 2c (Identification of methods in each class) and step 2d (Internal method design) of the Software Design phase in the Software Development Process presented in Chapter 2.

Consider a map represented in your source code by a class called Map. One of the services of this class is to calculate the distance between a list of 6 specified locations (here referred to as L1, L2, L3, L4, L5, and L6) on the map. Every location in the map constitutes a set of 2 coordinates (x and y), where L1 has the coordinates (x1, y1), L2 has the coordinates (x2, y2), and so on. The distance between two locations, say L1 (x1, y1) and L2 (x2, y2), can be calculated by using Pythagoras's formula:

which can be used to calculate the distance of a path beginning at L1 and going through L2, L3 and on to L6. The formula for this calculation is

Total distance =

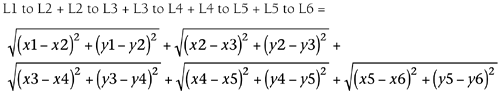
We can implement this distance calculation in two ways:

• By using just one method, without any attempt to break up the problem into a couple of simpler methods.

• By thinking in terms of methods as building blocks, we can divide the functionality into several methods.

To keep the examples simple, I will only provide the very important parts of the C# code.

Let's have a closer look at each implementation.

• By using only one method:

   totalDistance =     Math.Sqrt(Math.Pow(x1-x2,2) + Math.Pow(y1-y2,2)) +     Math.Sqrt(Math.Pow(x2-x3,2) + Math.Pow(y2-y3,2)) +     Math.Sqrt(Math.Pow(x3-x4,2) + Math.Pow(y3-y4,2)) +     Math.Sqrt(Math.Pow(x4-x5,2) + Math.Pow(y4-y5,2)) +     Math.Sqrt(Math.Pow(x5-x6,2) + Math.Pow(y5-y6,2)); 

  where Math.Sqrt(x) calculates the square root of x and Math.Pow(a, b) raises a to the power of b.

  This coding nightmare is one statement spread over six lines of source code. Let's try to simplify this massive statement.

• Breaking down the functionality into two methods:

  Because we are repeatedly calculating distances between two locations, we can separate the functionality into two methods a helper method calculating distances between two locations and a method calculating the total distance between the six locations. We will simply call our helper method Distance and let it contain four formal parameters a1, b1 (representing the first location) a2, b2 (representing the second location). When Distance is called, it returns the distance between the location arguments sent to it.

  We can now write the calculation in only four lines of code.

   TotalDistance =     Distance(x1,y1,x2,y2) + Distance(x2,y2,x3,y3) +     Distance(x3,y3,x4,y4) + Distance(x4,y4,x5,y5) +     Distance(x5,y5,x6,y6); 

In this way, we were able to obtain a significant reduction in the complexity of this calculation. Another advantage is that we don't have to remember Pythagoras's formula and try to get it right numerous times; instead, we simply need to call the Distance method.

Note

By implementing a class called Location to represent specific locations in the form of objects, naming these location objects L1, L2, and so on will reduce the previous statement to

 TotalDistance =     Distance(L1,L2) + Distance(L2,L3) +     Distance(L3,L4) + Distance(L4,L5) +     Distance(L5,L6); 

Indeed, this is a much simpler and self-documenting statement. To understand and construct this type of statement, we need to put more meat into your understanding for methods and OOP.

If none of our other objects in the program are interested in a Distance method, we need to make things less complex when looking at the class from the outside. As a result, we declare this helper method to be private.

As we attempt to reduce the complexity of the individual class by breaking its complicated tasks into subtasks, we also create the need for private methods.

Tip

A method attempting to solve several tasks is likely to be overly complex and should probably be broken down into smaller, simpler methods. So don't be afraid of creating many small methods.

A method that accomplishes one clear task is said to be cohesive.

A good guideline for whether you have created a set of cohesive methods is the ease with which you can name each method. Methods with one distinct task are easier to name than multipurpose methods.

---