Tool 43: Correlation Analysis

AKA

Hypothesis Testing (Correlation)

Classification

Decision Making (DM)

Tool description

The correlation analysis (hypothesis testing) procedure is utilized to measure the strength of the relationship or correlation (if any) between two variables or data sets of interest. A scatter diagram is usually completed to show, visually, the approximate correlation before the correlation coefficient is calculated.

Typical application

• To measure the strength of a relationship (correlation) between two variables of interest.

• To calculate the correlation coefficient in order to accept or reject the stated null hypothesis (H₀), or, in other words, to test whether or not a statistically significant relationship exists between two variables.

Problem-solving phase

	Select and define problem or opportunity
→	Identify and analyze causes or potential change
	Develop and plan possible solutions or change
	Implement and evaluate solution or change
→	Measure and report solution or change results
	Recognize and reward team efforts

Typically used by

1	Research/statistics
	Creativity/innovation
2	Engineering
	Project management
	Manufacturing
	Marketing/sales
	Administration/documentation
	Servicing/support
3	Customer/quality metrics
	Change management

links to other tools

before

• Data Collection Strategy

• Sampling Method

• Descriptive Statistics

• Scatter Diagram

• Standard Deviation

after

• Information Needs Analysis

• Trend Analysis

• Response Matrix Analysis

• SWOT analysis

• Presentation

Notes and key points

Sufficient supporting information is presented here to provide a good overview of the hypothesis testing procedure using a correlation test to illustrate the sequential steps involved to arrive at a decision. It is suggested, however, that the reader refer to a text on statistics for additional information and examples.

This is the recommended eight-step procedure for testing a null hypothesis (H₀)

(Note: Pearson's r, the product-moment correlation coefficient, is used for this example).

1. Data Source: Errors made in document processing

   • Variable X = number of documents processed per day

   • Variable Y = number of errors per day

2. Research and null hypothesis (H₁ - H₀)

   • H₁: There is a statistically significant relationship (correlation) in an increase of documents processed with an increase in errors per day.

   • H₀: There is no statistically significant relationship (correlation) in an increase of documents processed with an increase of errors per day measured at .05 level of significance using a Pearson's product-moment correlation test.

3. Test used: Simple PPM two-tailed correlation test.

4. Level of significance used: .05

5. Degree of freedom: 10 (n-2), 12 pairs in our example.

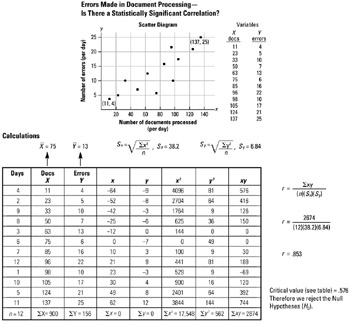
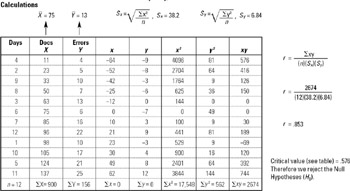
6. Test result: r = .853

7. Critical value: .576 (See Pearson's Table in the Appendix, Table E.)

8. Decision: Reject the H₀! (If the test result is higher than the critical value, the H₀ is rejected. The test result is in the rejection region under the curve.)

   • Pearson's product-moment equations:

     

Critical Values Table for Correlation Coefficient

No. of Pairs	(df)Degrees of Freedom	Level of Significance
		.20	.10	.05	.01	.001
3	1	0.951	.988	.997	1.000	1.000
4	2	0.800	.900	.950	.990	.999
5	3	0.687	.805	.878	.959	.991
6	4	0.608	.729	.811	.917	.974
7	5	0.551	.669	.755	.875	.951
8	6	0.507	.621	.707	.834	.925
9	7	0.472	.582	.666	.798	.898
10	8	0.443	.549	.632	.765	.872
11	9	0.419	.521	.602	.735	.847
12	10	0.398	.497	.576	.708	.823
13	11	0.380	.476	.553	.684	.801
14	12	0.365	.457	.532	.661	.780
15	13	0.351	.441	.514	.641	.760
16	14	0.338	.426	.497	.623	.742
17		0.327	.412	.482	.606	.725

Step-by-step procedure

• STEP 1 Data has been collected in order to check if there is any correlation in documents processed and errors found in processing. See example Errors Made in Document Processing—Is There a Statistically Significant Correlation?

• STEP 2 A scatter diagram is prepared as shown in this example.

• Note: Refer to scatter diagram in this book for additional information.

• STEP 3 Prepare a table for calculating the correlation coefficient r. Insert the data (docs and errors) into columns X and Y as shown.

  • Calculate the average of column X, and of column Y.

  • Subtract from X scores and get small x, the deviation score.

  • Subtract from Y scores and get small y, the deviation score.

  • Square small x to get x².

  • Square small y to get y².

  • Multiply small x times small y to get xy.

  • Total column xy and insert into r equation.

  • Note: Refer to standard deviation in this handbook to calculate the standard deviation S_x and S_y.

• STEP 4 Complete the calculations to get r, the correlation coefficient. Refer to the hypothesis testing steps as outlined in notes and key points on the previous page.

Example of tool application

Errors Made in Document Processing—

Is There a Statistically Significant Correlation?