7.4 Solving a Quadratic Equation
7.4 Solving a Quadratic Equation
A quadratic equation is a simple mathematical model of a second-degree equation. The goal of the problem is to compute the two roots of the equation.
7.4.1 Analysis of the Problem
Consider the problem of solving a quadratic equation (second-degree equation) of the form:
ax2 + bx + c = 0
The input values for this problem are the values of the coefficients of the quadratic equation: a, b, and c. The solution of this equation gives the value of the roots, x1 and x2.
7.4.2 Preliminary Design
If the value of a is not zero (a ≠ 0), the general expression for the value of the two roots is:
The expression inside the square root is called the discriminant. It is defined as: b2 - 4ac. If the discriminant is negative, the solution will involve complex roots. The solution discussed here only considers the case for real roots of the equation. Figure 7.5 shows the flowchart for the general solution.
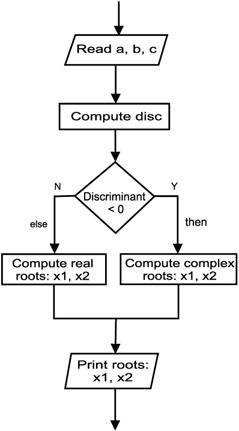
Figure 7.5: High-level flowchart for the quadratic equation.
Get the values of the coefficients a, b, and c Calculate value of the discriminant If the value of the discriminant is less than zero Then no calculations Else calculate the two real roots Show the value of the roots
7.4.3 Next-Level Design
The algorithm in the informal pseudo-code notation for the solution of the quadratic equation is:
Read the value of a from the input device Read the value of b from the input device Read the value of c from the input device Compute the discriminant, disc = b2 - 4ac, as an intermediate result if discriminant less than zero then roots are complex, no calculations else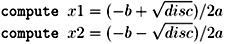 
endif Print values of the roots: x1 and x2 The algorithm is implemented in function main of class Quadra. It implements the data description and final design of the algorithm in KJP for the solution of the quadratic equation.
| On the CD | The code for the KJP implementation follows and is stored in the file |
description This program computes the solution for a quadratic equation; this is also called a second-degree equation. The program reads the three coefficients a, b, and c of type double; the program assumes a > 0. This is the main and the only class of this program. */ class Quadra is public description The control function for the program. */ function main is variables // coefficients: a, b, and c double a double b double c double disc // discriminant double x1 // roots for the equation double x2 begin display "Enter value of a" read a display "Enter value of b" read b display "Enter value of c" read c // Compute discriminant set disc = Math.pow(b,2) - (4*a*c) // Check if discriminant is less than zero if disc less than 0.0 then // not solved in this program display "Roots are complex" else // ok, compute both roots display "Roots are real" set x1 = ( -b + Math.sqrt(disc)) / (2.0 * a) set x2 = ( -b - Math.sqrt(disc)) / (2.0 * a) print "x1: ", x1 print "x2: ", x2 endif endfun main endclass Quadra
The KJP translator generates a Java file from a KJP file. In this case, the file generated is 
Quadra.java. The following code is the Java implementation of class Quadra.
// KJP v 1.1 File: Quadra.java, Fri Dec 06 19:47:10 2002 /** This program computes the solution for a quadratic equation; this is also called a second-degree equation. The program reads the three coefficients a, b, and c of type double; the program assumes a > 0. This is the main and the only class of this program. */ public class Quadra { /** The control function for the program. */ public static void main(String[] args) { // coefficients: a, b, and c double a; double b; double c; double disc; // discriminant // roots for the equation double x1; double x2; System.out.println("Enter value of a"); a = Conio.input_Double(); System.out.println("Enter value of b"); b = Conio.input_Double(); System.out.println("Enter value of c"); // // Compute discriminant c = Conio.input_Double(); // Check if discriminant is less than zero disc = Math.pow(b, 2) - (4 * a * c); if ( disc < 0.0) { // not solved in this program System.out.println("Roots are complex"); // ok, compute both roots } else { System.out.println("Roots are real"); x1 = - b + Math.sqrt(disc) /( 2.0 * a); x2 = - b - Math.sqrt(disc) /( 2.0 * a); System.out.println("x1: "+ x1); System.out.println("x2: "+ x2); } // endif } // end main } // end Quadra | On the CD | The Java implementation of class Quadra is stored in the file |
The execution of class Quadra is shown in Figure 7.6. The values for the coefficients are 2, 5, and 3 for a, b, and c, respectively.
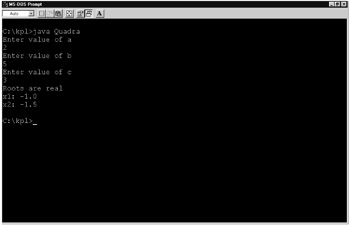
Figure 7.6: Execution of class Quadra for the quadratic equation.
EAN: 2147483647
Pages: 184