3. Probabilistic Modeling of Media Features

3. Probabilistic Modeling of Media Features

We presented a probabilistic architecture of multiject models representing sites, objects and events for capturing semantic representations [13,24]. Bayes decision theory [44] and statistical learning form the core of our architecture. We briefly review the characteristics and the assumptions of this architecture.

3.1 Probabilistic Multimedia Objects (Multijects)

Semantic concepts (in video) can be informally categorized into objects, sites and events. Any part of the video can be explained as an object or an event occurring at a site or location. Such an informal categorization is also helpful for selecting structures of the models, which are used to represent the concepts. For the automatic detection of such semantic concepts we propose probabilistic multimedia objects or multijects.

A multiject represents a semantic concept that is supported by multiple media features at various levels (low level, intermediate level, high level) through a structure that is probabilistic [13,30]. Multijects belong to one of the three categories: objects (car, man, helicopter), sites (outdoor, beach) or events (explosion, man-walking, ball-game). Figure 2.2 illustrates the concepts of a multiject.

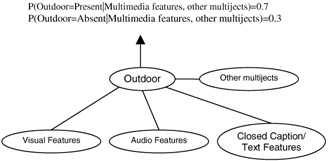
Figure 2.2: A probabilistic multimedia object (multiject).

A multiject is a flexible, open-ended semantic representation. It draws its support from low-level features of multiple media including audio, image, text and closed caption [13]. It can also be supported by intermediate-level features, including semantic templates [2]. It can also use specially developed high-level feature detectors like face detectors. A multiject can be developed for a semantic concept if there is some correlation between low-level multimedia features and high-level semantics. In the absence of such correlation, we may not be able to learn a sufficiently invariant representation. Fortunately many semantic concepts are correlated to some multimedia features, and so the framework has the potential to scale.

Multijects represent semantic concepts that have static as well as temporal support. Examples include sites like sky, water-body, snow, outdoor, explosion, flying helicopter, etc. Multijects can exist locally (with support from regions or blobs) or globally (with support from the entire video frame). The feature representation also corresponds to the extent of the spatiotemporal support of the multiject. We have described techniques for modeling multijects with static support in Naphade and Huang [24]. In this paper we concentrate on multiject models for events with temporal support in media streams.

3.2 Assumptions

We assume that features from audiovisual data have been computed and refer to them as X. We assume that the statistical properties of these features can be characteristic signatures of the multijects. For distinct instances of all multijects, we further assume that these features are independent identically distributed random variables drawn from known probability distributions, with unknown deterministic parameters. For the purpose of classification, we assume that the unknown parameters are distinct under different hypotheses and can be estimated. In particular, each semantic concept is represented by a binary random variable. The two hypotheses associated with each such variable are denoted by H_i, i∈ {0,1}, where 0 denotes absence and 1 denotes presence of the concept. Under each hypothesis, we assume that the features are generated by the conditional probability density function P_i(X), i∈ {0,1}. In case of site multijects, the feature patterns are static and represent a single frame. In case of events, with spatiotemporal support, X represents a time series of features over segments of the audiovisual data. We use the one-zero loss function [45] to penalize incorrect detection. This is shown in Equation 1:

(2.1)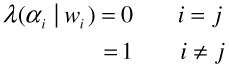

The risk corresponding to this loss function is equal to the average probability of error and the conditional risk with action α_i is 1-P(ω_i|x). To minimize the average probability of error, class ω_i must be chosen, which corresponds to the maximum a posteriori probability P(ω_i|x). This is the minimum probability of error (MPE) rule.

In the special case of binary classification, this can be expressed as deciding in favor of ω₁ if

(2.2)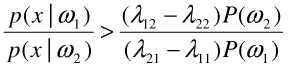

The term p(x|ω_j) is the likelihood of ω_j, and the test based on the ratio in Equation (2) is called the likelihood ratio test [44,45].

3.3 Multiject Models for Audio and Visual Events

Interesting semantic events in video include explosion, car chase, etc. Interesting semantic events in audio include speech, music, explosion, gunshots, etc. We propose the use of hidden Markov models for modeling the probability density functions of media features under the positive and negative hypotheses.

We model a temporal event using a set of states with a Markovian state transition and a Gaussian mixture observation density in each state. We use continuous density models in which each observation probability distribution is represented by a mixture density. For state j the probability b_j(o_t) of generating observation o_t is given by Equation (3):

(2.3)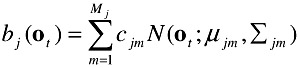

where M_j is the number of mixture components in state j, c_jm is the weight of the m^th component and N(o;μ,Σ) is the multivariate Gaussian with mean μ and covariance matrix Σ as in Equation (4):

(2.4)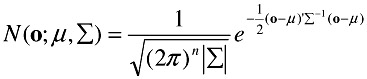

The parameters of the model to be learned are the transition matrix A, the mixing proportions c, and the observation densities b. With q_t denoting the state at instant t and q_t+1 the state at t+1, elements of matrix A are given by a_ij=P(q_t+1=j|q_t=i). The Baum-Welch re-estimation procedure [46,26] is used to train the model and estimate the set of parameters. Once the parameters are estimated using the training data, the trained models can then be used for classification as well as state sequence decoding [46,26]. For each event multiject, a prototype HMM with three states and a mixture of Gaussian components in each state is used to model the temporal characteristics and the emitting densities of the class. For each mixture, a diagonal covariance matrix is assumed.

We have developed multijects for audio events like human-speech, music [7] and flying helicopter [40], and visual events like explosion [13], etc.