Hack 39. Lose Slowly at Roulette

Roulette has so many pretty colors and shiny objects that kittens love it. Plus, you'll look pretty cool playing it. But in the long run, you'll lose money, and with your cat allergy and all....

Like most games in a casino, roulette is a game of pure chance. No one has any skill when it comes to predicting which of the 37 (European-style) or 38 (U.S.-style) partitioned sections the tiny ball will end up in. The best a player can do is know the odds, manage his money, and assume going in that he will lose.

Of course, he might get lucky and win some money, which would be dandy, but the Law of Big Numbers [Hack #2] must be obeyed. In the long run, he is most likely to have less money than if he had never played at all. In fact, if he plays an infinite amount of time, he is guaranteed to lose money. (Most roulette players play for a period of time somewhat less than infinity, of course.) To extend your amount of playing time, there is important statistical information you should know about this game with the spinning wheel, the orbiting ball, and the black and red layout.

Basic Wagers

Figure 4-1 shows the betting layout of a typical roulette game. This is an American-style layout, which means there are two green numbers, 0 and 00, which do not pay off any bets on red and black or odd and even. European-style roulette wheels have only one green number, 0, which cuts in half the house advantage compared to U.S. casinos.

Figure 4-1. Typical roulette betting layout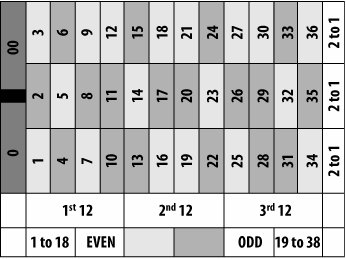

Players can bet in a large variety of ways, which is one reason roulette is so popular in casinos. For example, a player could place one chip over a single number, touching two numbers, on a color, adjacent to a column of 12 numbers, and so on. Like any other probability question, the chance of randomly getting the desired outcome is a function of the number of desired outcomes (winning) divided by the total number of outcomes.

There are 38 spaces on the wheel and, because all 38 possible outcomes are equally likely, the calculations are fairly straightforward. Table 4-10 shows the types of bets players can make, the information necessary to calculate the odds of winning for a single spin of the wheel and a one-dollar bet, the actual amounts the casino pays out, and the house advantage.

Table Statistics of roulette for each $1 bet

Type of wager	Number of winning outcomes	Number of losing outcomes	Odds	Casino pays	House edge equation	House edge
Single number	1	37	37 to 1	$35		5.26 percent
Two numbers	2	36	36 to 2 or18 to 1	$17		5.26 percent
Single color	18	20	20 to 18 or1.11 to 1	$1		5.26 percent
Even or odd	18	20	20 to 18 or1.11 to 1	$1		5.26 percent
Twelve numbers	12	26	26 to 12 or2.17 to 1	$2		5.26 percent

The house advantage is figured by first determining what the casino should pay back for each dollar bet if there were no advantage to the casino. The fair payback would be to give the winner an amount of money equal to the risk taken. The amount of risk taken is, essentially, the number of possible losing outcomes. This actual amount paid to the winner is then subtracted from the amount that should be paid if there were no house advantage. These "extra" dollars that the house keeps is divided by the proportion of total outcomes to winning outcomes. If there are no extra dollars, the game is evenly matched between player and casino and the house edge is 0 percent.

If you study the statistics of roulette in Table 4-10, a couple of conclusions are apparent. First, the casino makes its profit by pretending that there are only 36 numbers on a roulette wheel (i.e., only 36 possible outcomes) and pays out using that pretend distribution.

Second, regardless of the type of wager that is made at a roulette wheel, the house edge is a constant 5.26 percent. This is true except for one obscure wager, which is allowed at most casinos. Players are often allowed to bet on the two zeros and their adjacent numbers, 1, 2 and 3, for a total of five numbers. This is done by placing a chip to the side, touching both the 0 and the 1. I'd tell you more about checking with the person who spins the wheel to make sure they take this wager, and so on, except that this is the worst bet at the roulette table and no statistician would advise it. Casinos who allow this bet pay out as if it were a bet on six numbers. So, the casino's usual edge of 5.26 percent is even larger here: 7.89 percent, as shown in Table 4-11.

Table Statistics for betting on five numbers in roulette (an inadvisable wager)

Type of wager	Number of winning outcomes	Number of losing outcomes	Odds	Casino pays	House edge equation	House edge
Five numbers	5	33	33 to 5 or6.6 to 1	$6		7.89 percent

Why It Works

Roulette's popularity is based partly on the fact that so many different types of wagers are possible. A gambler with a lot of chips can spread them out all over the table, with a wide variety of different bets on different numbers and combinations of numbers. As long as she avoids the worst bet at the table (five numbers), she can rest assured that the advantage to the house will be the same honest 5.26 percent for each of her bets. It is one less thing for the gambler to worry about.

The fact that there is such a large variety of bets that can be placed on a single layout is no lucky happenstance, though. The decision to use 36 numbers was a wise one, and no doubt it was made all those years ago because of the large number of factors that go into 36. Thirty-six can be evenly divided by 1, of course, but also by 2, 3, 4, 6, 9, 12, and 18, making so many simple bets possible.