Hack 23. See the Shape of Everything

Almost everything in the natural world is distributed in the same way. As long as you can measure the thing, whatever it is, and scores are allowed to vary, it has a well-defined "normal distribution." If you know the specifics about the shape of this normal curve, you can make very accurate predictions about performance.

There are a few miracles in the world of statistics. There are at least three toolsthree discoveriesthat are so cool and magical that once students of statistics learn about them and begin to comprehend their beauty, they frequently explode.

Well, maybe I am exaggerating a bit, but here are three dandy tools for understanding the world:

• The correlation coefficient [Hack #11]

• The Central Limit Theorem [Hack #2]

• The normal curve

Since we've discussed the uses of the first two miracles in other hacks, let's spend our time now getting to know the shape and uses of the third: the normal curve. I am pleased to present the normal curve, the normal distribution, the bell-shaped curve, the whole world, as shown in Figure 3-1.

Figure 3-1. The normal curve

Applying Areas Under the Normal Curve

Statisticians have defined the normal curve very specifically. Using both calculus and hundreds of years of real-world data collection, the two methods have reached the same set of conclusions about the exact shape of the normal distribution. Figure 3-2 shows the important characteristics of the normal curve. The mean is in the middle, and there is room for fewer and fewer scores as you move away from that center.

Figure 3-2. Areas under the normal curve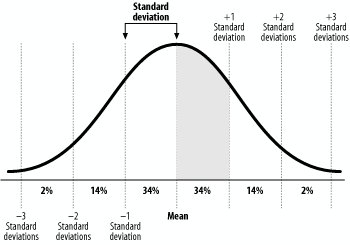

Though the normal curve is theoretically infinitely wide, three standard deviations on either side of the mean is usually enough to contain all the scores.

A distribution's standard deviation is the average distance of each score from the mean [Hack #2].

Predicting test performance

Recall the claim I made earlier that anything you measure will distribute itself as a normal curve. By implication, then, anything we measure will have most of the scores close to the mean and only a few scores far from the mean. Measure enough people and you will get the occasional extreme score very far from the mean, but scores far from the mean will be rare. The expected proportion of people getting any particular score gets smaller as that score moves away from the mean.

That next test you take? I don't know the test or anything about you, but I am willing to wager that you will get a score close to the mean. I predict your score will be average. You might get above average or below average, but the normal curve tells me that you will likely be pretty close to the mean.

To make these sorts of predictions, and to be pretty confident about their accuracy, you can use the known normal curve's dimensions to estimate the percentage of scores that will fall between any two points on the X-axis (the bottom, horizontal part of the graph). The percentage of scores between pairs of standard deviation points on the scale are shown in Figure 3-2. The percentages add up to 100 percent, but that is because of rounding. Remember that some scores, though just a few, will be further than three standard deviations away from the mean.

Here are some key facts about the curve that you can use to predict performance:

• About 34 percent of scores fall between the mean and one standard deviation above the mean. See the shaded section in Figure 3-2? If you took some ink and colored in the entire space beneath the normal curve, you would use 34 percent of the ink on this section.

• About 34 percent of scores fall between the mean and one standard deviation below the mean.

• About 14 percent of scores fall between one and two standard deviations above the mean.

• About 2 percent of scores fall between two and three standard deviations below the mean.

You can also combine the percentages to make other statements such as:

• About 68 percent of all scores will be within one standard deviation of the mean.

• About 50 percent of scores will be below the mean.

You can use these known percentages to make predictions and statements of probability. We can speak of the normal curve as either the percentage of scores that fall under given areas on the curve or the likelihood that any given test taker will fall under given areas:

• There is a 2 percent chance that you will score more than two standard deviations above the mean on your next test.

• There is only a 16 percent chance that this applicant will score lower than one standard deviation below the mean on our job skills test.

Setting standards

Policy makers rely on the assumption that ability is normally distributed when they establish levels of performance. They choose levels of performance that will guarantee them a certain percentage of qualifying people. The normal distribution is an invaluable tool for setting policy for admissions or services if one wants to magically know ahead of time how many people will qualify.

For example, a college with high academic standards might require scores on an ability test that are at least one standard deviation above the mean. This way, they ensure themselves of accepting only the top 16 percent in ability.

Likewise, special education policy in the United States establishes certain cut scores for students on tests that qualify them for special education status (and, thus, federal and state funding). Cut scores are specific scores that a person must score above (or below). If policy makers have the budget to pay for special programming and staff for only, say, two percent of all children, they set the cut score at two standard deviations below the mean. Faith in the normal curve allows them to calculate the number of children who will need funding.

Appreciating the Beauty of the Normal Curve

To appreciate the wonder of the normal distribution, you can always build your own. Imagine you measured something (such as attitude, knowledge, height, or speed). You have some scoring system in which scores are allowed to vary (such as scores on an attitude survey, or SAT scores, or inches, or miles per hour). You have lots of scores because you measured lots of people, buildings, or sparrows. Now, plot these scores on a graph such that the X-axis represents the actual score value from lowest to highest, left to right (or the other direction if you'd like). The Y-axis (the vertical left side part) should represent the relative frequency of each value in your group of scores.

On such a chart, the height of the line or dot represents the relative proportion of scores that were at any particular value. Notice on the normal curve that the highest points are in the middle and the lowest points are on the ends. The middle score is the average score and the most popular score. On the normal curve, the median is equal to the mean, which is equal to the mode [Hack #21].

Notice also that the normal curve is symmetrical: you could fold it in half and one side would perfectly cover the other. The other characteristic of the normal curve that is important to know is that it goes on forever. It is a theoretical curve, so the two ends of the curve will never touch the baseline.

The normal curve is the common truth that connects all of nature. It is perfectly balanced. It is forever. It is eternal. It also kind of looks like a dinosaur, which is cool.