Section 10.5. Additive Synthesis
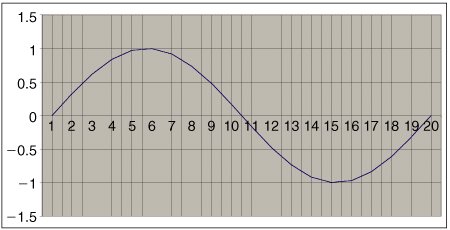
10.5. Additive SynthesisAdditive synthesis creates sounds by adding sine waves together. We saw earlier that it's really pretty easy to add sounds together. With additive synthesis, you can shape the waves yourselves, set their frequencies, and create "instruments" that never existed. 10.5.1. Making Sine WavesLet's figure out how to produce a set of samples to generate a sound at a given frequency and amplitude. From trigonometry, we know that if we take the sine of the radians from 0 to 2p, we'll get a circle. Spread that over time, and you get a sine wave. In other words, if you took values from 0 to 2p, computed the sine of each value, and graphed the computed values, you'd get a sine wave. From your math courses, you know that there's an infinity of numbers between 0 and 1. Computers don't handle infinity very well, so we'll actually only take some values between 0 to 2p. To create the following graph, Mark filled 20 rows (a totally arbitrary number) of a spreadsheet with values from 0 and 2p (about 6.28). Mark added about 0.314 (6.28/20) to each preceding row. In the next column, he took the sine of each value in the first column, then graphed it.
Let's say that we want to create a sound at a given frequency, say 440 Hz. This means that we have to fit an entire cycle like the above into 1/440 of a second. (440 cycles per second, means that each cycle fits into 1/440 second, or 0.00227 seconds.) Mark made the above picture using 20 values. Call it 20 samples. How many samples do we have to chop up the 440 Hz cycle into? That's the same question as: How many samples must go by in 0.00227 seconds? We know the sampling ratethat's the number of samples in one second. Let's say that it's 22,050 samples per second (our default sampling rate). Each sample is then (1/22,050) 0.0000453 seconds. How many samples fit into 0.00227? That's 0.00227/0.0000453, or about 50. What we just did here mathematically is:
Now let's spell this out in Java code. To get a waveform at a given frequency, say 440 Hz, we need 440 of these waves in a single second. Each one must fit into the interval of 1/frequency. The number of samples that needs to be produced during the interval is the sampling rate divided by the frequency, or interval (1/f) * (sampling rate). Call that the samplesPerCycle. At each entry of the sound sampleIndex, we want to:
10.5.2. Creating Sounds Using Static MethodsAll of the methods that we have written work with an existing object. But if the method we want to write this time creates the object, there won't be a current object to modify. How can we invoke this method if we don't have an object of the class to invoke it on? We can use a class method. A class method is also called a static method. Class methods can be called using ClassName.methodName(parameterList). Recall that when a class definition is compiled it creates a file (ClassName.class) that contains all the information in the class definition in a form that the computer can understand. When you use a class name for the first time in your code or in the interactions pane, Java looks for that file and loads the definition of that class. It also creates an object that represents that class. We have been using new Class(parameterList) to create new objects of the class by asking that object that represents the class to create an object for us. Now we will use ClassName.methodName(parameterList) to ask the object that represents the class to create an object of that class and return it. How do we make a method a class method? We add the keyword static to it, usually after the visibility (i.e., public, private). Now when you hear "static" you may think of noise on your radio or that something won't move. But in Java "static" means something that exists in the object that represents the class. So why not use "class" instead of "static"? The keyword class is used in Java to define new classes. But when you see the keyword static think class. So the keyword static in a method declaration tells you that the method is a "class" method. To build sounds, there are some silent sounds in the media sources. Our sine wave generator will use the one second of silence sound to build a sine wave of one second. We'll provide an amplitude as inputthat will be the maximum amplitude of the sound. (Since sine generates between 1 and 1, the range of amplitudes will be between amplitude and amplitude.) Program 88. Generate a Sine Wave at a Given Frequency and Amplitude
Notice that this method creates an object of the Sound class and returns it. In order to be able to refer to this Sound object again be sure to set a variable to refer to it. We can invoke any class method using ClassName.methodName(parameterList). Let's build a sine wave of 880 Hz at an amplitude of 4,000 (Figure 10.5). > Sound s = Sound.createSineWave(880,4000); > s.explore(); Figure 10.5. The sine wave with a frequency of 880 and a maximum amplitude of 4,000.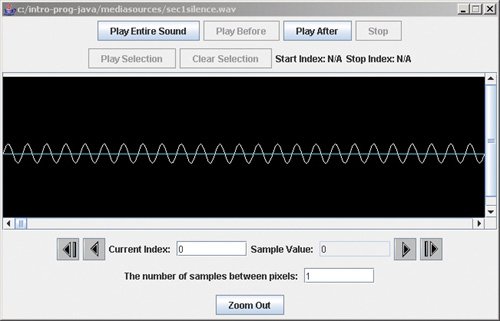 10.5.3. Adding Sine Waves TogetherNow let's add sine waves together. As we said at the beginning of the chapter, that's pretty easy: Just add the samples at the same indices together. Here's a method that adds one sound into a second sound. Program 89. Add Two Sounds Together
How are we going to use this method to add together sine waves? We need both of them at once? Turns out that it's easy: Let's add together 440 Hz, 880 Hz (twice 440), and 1,320 Hz (880 + 440), and we'll increase the amplitudes. We'll double the amplitude each time: 2,000, then 4,000, then 8,000. We'll add them all up into a sound called sound440. At the end, we generate a 440 Hz sound so that we can listen to them both and compare. > Sound s440 = Sound.createSineWave(440,2000); > Sound s880 = Sound.createSineWave(880,4000); > Sound s1320 = Sound.createSineWave(1320,8000); > s440.add(s880); > s440.add(s1320); > s440.explore(); > Sound orig440 = Sound.createSineWave(440,2000); > orig440.explore();
10.5.4. Checking our ResultHow do we know if we really got what we wanted? We can test our code by using the sound tools in the MediaTools. First we save out a sample wave (just 440 Hz) and the combined wave. > orig440.write(FileChooser.getMediaPath("just440.wav")); > s440.write(FileChooser.getMediaPath("combined440.wav"));Open up each of these in turn in the sound editor. Right away, you'll notice that the wave forms look very different (Figure 10.6). That tells you that we did something to the sound, but what? Figure 10.6. The raw 440 Hz signal on top, then the 440 + 880 + 1,320 Hz signal on the bottom.
The way to really check your additive synthesis is with a fast fourier transform (FFT). Generate the FFT for each signal. You'll see that the 440 Hz signal has a single spike (Figure 10.7). That's what you'd expectit's supposed to be a single sine wave. Now, look at the combined wave form's FFT (Figure 10.8). It's what it's supposed to be! You see three spikes there, and each succeeding one is double the height of the last one. Figure 10.7. FFT of the 440 Hz sound.
Figure 10.8. FFT of the combined sound.
10.5.5. Square WavesWe don't have to just add sine waves. We can also add square waves. These are literally square-shaped waves, moving between +1 and 1. The FFT will look very different, and the sound will be very different. It can actually be a much richer sound. Try this method instead of the sine wave generator and see what you think. Note the use of an if statement to swap between the positive and negative sides of the wave halfway through a cycle. Program 90. Square Wave Generator for Given Frequency and Amplitude |
 /** * Method to generate a 1 second sound with square waves * with the passed frequency and maximum amplitude. * @param freq the desired frequency * @param maxAmplitude the maximum amplitude * @return the created sound */ public static Sound createSquareWave(int freq, int maxAmplitude) { Sound s = new Sound(FileChooser.getMediaPath("sec1silence.wav")); double samplingRate = s.getSamplingRate(); int value = 0; double interval = 1.0 / freq; // length of cycle in seconds double samplesPerCycle = interval * samplingRate; double samplesPerHalfCycle = (int) (samplesPerCycle / 2); |
Use it like this:
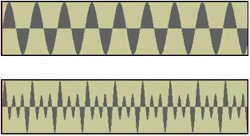
> Sound sq440 = Sound.createSquareWave(440,4000); > sq440.play(); > Sound sq880 = Sound.createSquareWave(880,8000); > Sound sq1320 = Sound.createSquareWave(1320,10000); > sq440.write(FileChooser.getMediaPath("square440.wav")); > sq440.add(sq880); > sq440.add(sq1320); > sq440.play(); > sq440.write(FileChooser.getMediaPath("squareCombined.wav"));You'll find that the waves (in the wave editor of MediaTools) really do look square (Figure 10.9), but the most amazing thing is all the additional spikes in FFT (Figure 10.10). Square waves really do result in a much more complex sound.
Figure 10.9. The 440 Hz square wave (top) and additive combination of square waves (bottom).

Figure 10.10. FFT's of the 440 Hz square wave (top) and additive combination of square waves (bottom).

10.5.6. Triangle Waves
Try triangle waves instead of square waves with this method.
Program 91. Generate Triangle Waves (This item is displayed on pages 332 - 333 in the print version)
 /** * Method to create a one second triangle wave sound * with the given frequency and maximum amplitude * @param freq the desired frequency * @param maxAmplitude the maximum amplitude * @return the new sound */ public static Sound createTriangleWave(int freq, int maxAmplitude) { Sound s = new Sound(FileChooser.getMediaPath("sec1silence.wav")); double samplingRate = s.getSamplingRate(); int value = 0; double interval = 1.0 / freq; // length of cycle in seconds double samplesPerCycle = interval * samplingRate; int samplesPerQuarterCycle = (int) (samplesPerCycle / 4); int increment = (int) (maxAmplitude / samplesPerQuarterCycle); // loop through the length of the sound for (int soundIndex = 0; soundIndex < s.getLength(); soundIndex++, value = value + increment) { |
Since this is a class method it can be invoked using
ClassName.methodName(parameterList). > Sound triangle = Sound.createTriangleWave(440,4000); > triangle.play(); > triangle.explore();
You have seen other class (static) methods. What about Math.abs(int number), FileChooser.pickAFile(), and ColorChooser.pickAColor()? All of these are class methods which is why you can invoke them using
ClassName.methodName(parameterList).
Class methods are useful for general methods that don't require an object of the class to be created (Math.abs) or for methods that create objects of the class, like createTriangleWave.
EAN: N/A
Pages: 191