4 Propagation channel properties

These various paths of different amplitude and phase interfere while arriving at the receiver. The interferences are constructive (the different paths arrive in phase) leading to signal reinforcement or destruction; one then has signal fade. Moreover, it should be noted that the mobile moves in this figure of interferences . It sees successively luminous and dark patches (interference fringes) causing fading of the signal.

Because of the presence of multiple paths and displacement of the receiver, the propagation channel has three fundamental properties: attenuation, variability and selectivity in frequency.

In analogical communication, the attenuation concept was sufficient to study the propagation channel. In the context of numerical communication, fading due to variability and the selectivity induce deterioration of the quality of the communication independently of attenuation.

4.1 Attenuation

We generally distinguish the free-space attenuation and the attenuation relative to free-space (excess attenuation)

Attenuation in free-space (loss transmission) is due the dispersion of energy in the vacuum as it moves away from the transmitter. It is given by the following relation:

where:

d is the distance between the transmitter and the receiver,
» is the wavelength,
f is the frequency.

Example:

d = 1 km
f = 900 MHz, A = 91.4 dB
f = 1800 MHz, A = 97.4 dB

This supposes that one has only one radioelectric path whose 1st Fresnel ellipsoid is not obstructed. It attenuation is governed by the 1/d ² law (energy conservation). That means that we lose 6 dB each time the distance is doubled .

Attenuation relative to free-space attenuation is the difference between the basic transmission loss and the free-space basic transmission loss expressed in decibels; this due to absorption by gases, the hydrometeors, the walls, the vegetation, attenuation by diffraction , etc.

4.2 Variability

The propagation environment fluctuates: the passage of vehicles and people, the wind in the trees, the opening of doors cause fluctuations of the radioelectric paths and generate fast variations the observed signal. Combined with the movement of vehicles, these phenomena create a variability of propagation in space and time.

The variations of the signal are of random nature. Statistical analysis will make it possible to evaluate the impact of the multiple paths on the transmission of radio-mobiles systems. The law of the field received and the fading average time for example are essential data to dimension the transmission equipment and their ability to fight against fading (interlacing, diversity).

Modelling of the fast variations was proposed [CLARKE, 1968]. By supposing that the mobile moves in an interference figure generated by the superposition of a great number of plane waves of amplitudes, independent phases and random directions, the field received (the complex envelop ) is, by the application of the theorem of the central limit, a Gaussian variable. The narrow band signal envelope, the power received, then follows a Rayleigh distribution. One speaks about Rayleigh fading .

In the case of a predominant path (line of sight, open environments such as suburbs, railway stations , rural areas, etc), the narrow band signal envelope, the received power, then follows a Rice distribution. This is observed when one of the paths is predominant. The Rice distribution corresponds to a Rayleigh distribution when r = 0 (absence of direct path) and makes it possible to identify a direct path and its preponderance. It is also characterised by the K coefficient (Rice parameter) defined by the relation:

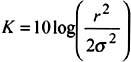
The K parameter represents the relation between the power of the direct path and the contribution to power in the secondary paths following a Rayleigh distribution.

The larger the parameter K, the more important the direct path is in comparison with the multiple paths and the clearer the connection is. Conversely, if the predominant path is weak, (K ‰ ˆ’ 5 dB) one considers that the Rice distribution is identified with a Rayleigh distribution [CCIR, 1990]. The K value depends on the environment (dense urban, suburban, rural, etc).

Others distributions, such as those of Weilbull and Nakagami [BRAUN, 1991] also make it possible to characterise the radiomobile signal envelope.

In order to determine the variation law followed by the signal one applies statistical tests for example the Kolmogorov-Smirnov test [BARBOT, 1992] to its fast variations resulting from the interference of the waves received.

Knowing the statistical characteristics of the signal (density of probability, function of distribution), makes it possible to determine the relevant parameters of a radioelectric system operation among which:

probability of going below a certain level. When the signal power is lower than the noise threshold tolerated by the receiver (thermal noise, jamming, industrial parasites, etc), the signal is mothered by the noise. The receiver is then unable to correctly interpret the transmitted information.
statistical fading duration. During fading, information packages are lost. The slower the mobile moves, the longer the cut-off times.

4.3 Selectivity

When the differences of the multiple paths delays are important, the transfer function is not constant over all the width of the spectrum: the path loss depends on the frequency used. The channel is known as selective in frequency .

Wideband modelling of the channel is then essential to evaluate the performance of a complete transmission chain, to conceive the new systems and to ensure the transmission quality of transmission of numerical signals.

The radioelectric channel is represented by its variable impulse response in time, h(t ˆ’ ), being the delay and t pointing out the dependence on time (and thus in space since the vehicle moves). A function of two variables , it translates the three characteristics of the channel: the attenuation, the variability (t) and the selectivity ( ).

The dual variables, by Fourier transform of and t are respectively the frequency and Doppler speed [PARSONS, 1992], [KATTERBACH, 1995].

The output signal y(t), as a function of the input signal x(t), is represented in the form of an equation of convolution whose convolution core is variable in time:

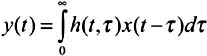
where h(t ˆ’ ) is the impulse response at the moment t to a radioelectric impulse x(t) which one would have emitted at the moment t ˆ’ . It completely defines the propagation channel. It makes possible to distinguish the various echoes according to their delays from propagation.

It is useful to qualify the selectivity of the channel by parameters deduced from the average profile of power of the impulse response. The most used are the mean delay, the rms delay spread, the delay interval, the delay window and the coherence bandwidth of the channel [FAILLY, 1989].

4.3.1 Average delay profile

One defines the average delay profile P( ) of the impulse response from h(t ˆ’ ) by the relation:

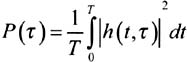
It corresponds to an average over a certain duration T (Figure 14.3) selected so that the measured impulse responses can be presented as a stationary and an ergodic random process [LAVERGNAT, 1997].

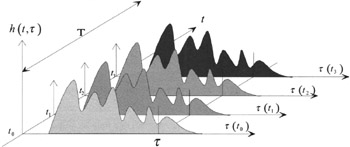
Figure 14.3: Schematic representation of the temporal evolution of the impulse response of the propagation channel

4.3.2 Average delay

The average delay is the average of the delays weighted by their power. It is given by the first moment of the impulse response:

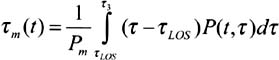
where:

_LOS is the delay of the line of sight path,
₃ is the instant when P( ) exceeds the cut-off level for the last time,
P _m is the total energy of the impulse response, defined by the following relation:

where:

P(t, )is the power density of the impulse response,
is the excess delay,
is the instant when P( ) exceeds the cut-off level for the first time.

4.3.3 The rms delay spread

The rms delay spread is the power weighted standard deviation of the excess delays. It characterises the variability of the rms mean delay. It is given by the second moment of the impulse response:

The rms delay spread illustrates the risk of appearance of intersymbol interferences and the disturbing effects that the remote and powerful echoes are likely to generate.

4.3.4 The delay interval

The delay interval at X dB is defined as the time interval between the time ₁ when the amplitude of the impulse response exceeds for the first time a given threshold and the time ₂ when this amplitude becomes for the last time lower than this threshold (Figure 14.4).

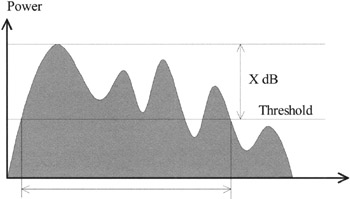
Figure 14.4: Example of power delay profile: highlighting of the delay interval at X dB

4.3.5 The delay window

The delay window is the duration of the central portion ( ₂ ˆ’ ₁ ) containing y % of the total energy found in the impulse response. Times ₁ and ₂ are defined by the relation (Figure 14.5):

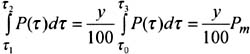
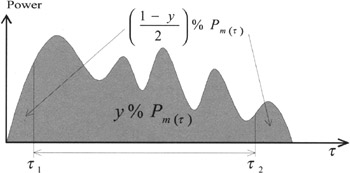
Figure 14.5: Example of power delay profile; highlighting of the delay window containing y% of the total energy found in the impulse response

4.3.6 The correlation bandwidth

The correlation bandwidth (Bc) of the channel is defined in the following way. Let C(t,f) be the autocorrelation of the transfer function (Fourier Transformation of the power of the impulse response).

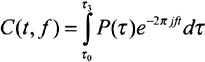
The correlation bandwidth is defined as the frequency for which C(t,f) is equal to X % of C(t,f=0) [PARSONS, 1992]. It indicates the amplitude of selective attenuation depending on separation in frequency. The correlation band is thus the frequency from which the autocorrelation function of the transfer function falls below a given threshold.

For the analysis of the experimental data, the UIT-R recommends use of delay intervals for thresholds of 9, 12 and 15 dB below the peak value, the delay windows for 50%, 75% and 90% of energy and a correlation bandwidth for 50% and 90% correlation.

The correlation bandwidth is linked to the delay spread by the following relation [LEE, 1993]:

The propagation channel is more or less selective according to the environment. The form of the impulse response is also different according to the environment. In pico cell environments (inside buildings ), the decrease of the power with respect to delay on the impulse response is exponential whereas in small and micro cells important delays are very clearly distinguished. One will note, in Figure 14.6, that the time scales are not the same for a pico cell and for small and micro cell environments.

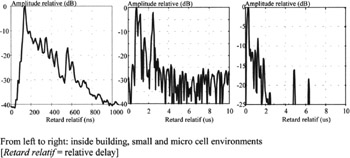
Figure 14.6: Examples of impulse responses measured in various environments