3 Mechanisms of propagation

Propagation paths (Figure 14.2) are of a different nature: direct, transmitted, reflected, scattered , diffracted or guided.

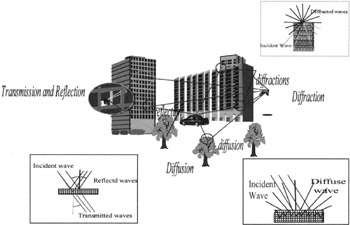
Figure 14.2: Various mechanisms of propagation

3.1 Direct paths

A path is known as direct when the transmitter and the receiver are in radioelectrical visibility (in line of sight): the first Fresnel ellipsoid is not obstructed. This ellipse delimits space area through which nearly all the energy passes . It is the place of the M points which fulfills the following equation (E indicates the site of the transmitter, R that of the receiver, » is the wavelength):

3.2 Transmitted paths

Most of the time the direct path does not exist: it is blocked by obstacles (masks). Transmission is a phenomenon which allows waves to cross an obstacle (wall, building, vegetation, etc).

3.3 Reflected paths

Reflection occurs when the wave meets a surface whose dimensions are large in comparison with the wavelength (ground, wall, fa §ade of building etc).

The reflection characteristics of an unspecified surface depend on several factors: the surface of the material (smooth or rough), the wavelength and the incidence angle.

The roughness of a surface relative to the wavelength constitutes an important parameter for the shape of the reflection diagram. A smooth surface reflects the incident radiation in only one direction as a mirror (specular reflection). On the contrary, a rough surface will reflect the incident radiation in all the directions.

A surface is regarded as rough, according to the Rayleigh criterion, if the following relation is satisfied:

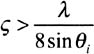
where:

is the maximal height of the surface irregularities,
» is the incident radiation wavelength,
_i is the incidence angle.

For an infrared radiation characterised by a wavelength of 1550 nm, under normal incidence, a surface is known as rough if the maximum height of the irregularities is greater than 0, 19 ¼ m. This result shows that the majority of surfaces met inside buildings are regarded as rough with infrared radiation; the diagram of reflection then presents a diffuse component (diffuse reflection).

3.3.1 Specular reflection

Specular reflection, a phenomenon common to all the frequencies, is due to a perfectly plane homogeneous surface. The loss path induced by such reflections arises from the Fresnel relations and depends on the dielectric characteristics of the reflective surface (conductivity ƒ , permittivity µ ). For example, the majority of surfaces inside the buildings have a reflection coefficient, in the infrared band , ranging between 0.4 and 0.9 [GFELLER, 1979]. Various reflection coefficients have been mentioned in the literature for different materials [YANG, 2000].

3.3.2 Diffuse reflection

Diffuse reflection is due to the reflections by surfaces which are not plane but rough; such surfaces present irregularities. The, an incident wave is not reflected in only one direction but diffused in multiple directions. Two models are usually used to represent reflection of the infrared band: Lambert and PHONG model.

Lambert model

Some surfaces are very irregular and reflect the infrared radiation in all the directions independently of the incidental radiation. Such surfaces are known as diffuse and can be represented by the Lambert model. The model is very simple and very easy to implement inside software. It is described by the following equation:

where:

is the surface reflection coefficient,
R _i represents the incident optical power,
is the observation angle.

Phong model

The reflection diagram of several rough surfaces is well represented by the Lambert model except around specular reflection where the experimental diagram presents an important component. The Phong model considers the reflection diagram as the sum of two components: diffuse and specular components . The percentage of each component, depending mainly on the surface characteristics is a parameter of the model. The diffuse component is given by the Lambert model. The specular component is given by a function which depends on the angle of incidence _i and the angle of observation (angle of reflection) . The Phong model is described by the following relation:

where:

is the surface reflection coefficient,
R _i represents the incident optical power,
r _d is the percentage of the ray which is considered in diffuse form (it is a value ranging between 0 and 1),
m is a parameter which controls the directivity of the specular component of the reflection,
_i is the incidence angle,
is the observation angle.

It will be noted that the Lambert model is equal to Phong's by taking rd equal to one. The Phong model, dependent on the observation and incidence angle, is more complex than Lambert's. The computing times are lengthened. The reflection pattern presents a principal lobe centered around the direction of the specular reflection.

3.4 Diffracted paths

Diffractions occur when a wave meets an edge (hill, building, vegetation, roofs, corners of buildings, road structures etc.) whose dimensions are large compared to the wavelength. It constitutes one of the most important factors intervening in the propagation of radio waves [BOITHIAS, 1983]. The use of the geometrical theory of diffraction (TGD) makes possible to represent this phenomenon in the form of rays [McNAMARA, 1990]. Approximate expressions were proposed for attenuation evaluation by diffraction [BOITHIAS, 1983]:

for v > ˆ’ 0.7 and is usable in the vicinity of 0.

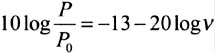
valid for v > 1,5

where:

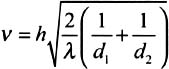
d ₁ and d ₂ are respectively the distances from the edge to the transmitter and the receiver.

The reader will find hereafter, as an example, some typical values of attenuation at 4 frequencies (20, 40, 60 and 100 GHz) for edges (of height 1 and 10 m) located at 1 km of the transmitter and receiver.

The results are summarized below.

Table 14.1: Typical values of attenuation by diffraction (in dB)
Diffraction attenuation (dB)	d=1 km, h=1m	d=1km, h=10m
Frequency = 20 GHz	10	30.3
Frequency = 40 GHz	14	33.3
Frequency = 60 GHz	16	35
Frequency = 100 GHz	18	37

3.5 Guided paths

Certain environments (deep streets (street canyons), corridors, tunnels, etc.) behave like true waveguides with respect to the propagation of the radiowaves consecutively to multiple successive reflections on the walls (application of propagation modes and ray theory more particularly when the wavelength is very small compared to the transverse section of the tunnel, for example).