2.8 REGULAR SETS AND REGULAR EXPRESSIONS

2.7 EXAMPLES OF FINITE AUTOMATA CONSTRUCTION

EXAMPLE 2.3

Construct a finite automata accepting the set of all strings of zeros and ones, with at most one pair of consecutive zeros and at most one pair of consecutive ones.

 

A transition diagram of the finite automata accepting the set of all strings of zeros and ones, with at most one pair of consecutive zeros and at most one pair of consecutive ones is shown in Figure 2.11.

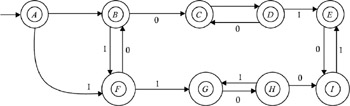
Figure 2.11: Transition diagram for Example 2.3 finite automata.

EXAMPLE 2.4

Construct a finite automata that will accept strings of zeros and ones that contain even numbers of zeros and odd numbers of ones.

 

A transition diagram of the finite automata that accepts the set of all strings of zeros and ones that contains even numbers of zeros and odd numbers of ones is shown in Figure 2.12.

Figure 2.12: Finite automata containing even number of zeros and odd number of ones.

EXAMPLE 2.5

Construct a finite automata that will accept a string of zeros and ones that contains an odd number of zeros and an even number of ones.

 

A transition diagram of finite automata accepting the set of all strings of zeros and ones that contains an odd number of zeros and an even number of ones is shown in Figure 2.13.

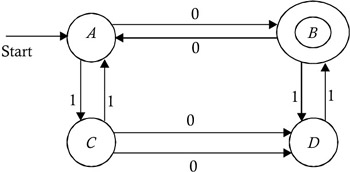
Figure 2.13: Finite automata containing odd number of zeros and even number of ones.

EXAMPLE 2.6

Construct the finite automata for accepting strings of zeros and ones that contain equal numbers of zeros and ones, and no prefix of the string should contain two more zeros than ones or two more ones than zeros.

 

A transition diagram of the finite automata that will accept the set of all strings of zeros and ones, contain equal numbers of zeros and ones, and contain no string prefixes of two more zeros than ones or two more ones than zeros is shown in Figure 2.14.

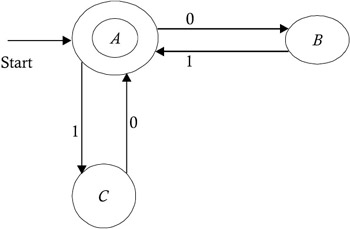
Figure 2.14: Example 2.6 finite automata considers the set prefix.

EXAMPLE 2.7

Construct a finite automata for accepting all possible strings of zeros and ones that do not contain 101 as a substring.

 

Figure 2.15 shows a transition diagram of the finite automata that accepts the strings containing 101 as a substring.

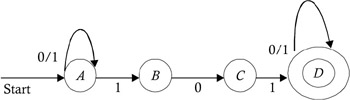
Figure 2.15: Finite automata accepts strings containing the substring 101.

A DFA equivalent to this NFA will be:

		1
{ A }	{ A }	{ A , B }
{ A , B }	{ A , C }	{ A , B }
{ A , C }	{ A }	{ A , B , D }
{ A , B , D }*	{ A , C , D }	{ A , B , D }
{ A , C , D }*	{ A , D }	{ A , B , D }
{ A , C , D }*	{ A , D }	{ A , B , D }

Let us identify the states of this DFA using the names given below:

{ A }	q
{ A , B }	q 1
{ A , C }	q 2
{ A , B , D }	q 3
{ A , C , D }	q 4
{ A , D }	q 5

The transition diagram of this automata is shown in Figure 2.16.

Figure 2.16: DFA using the names A-D and q _{ˆ’ 5} .

The complement of the automata in Figure 2.16 is shown in Figure 2.17.

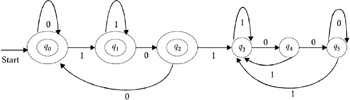
Figure 2.17: Complement to Figure 2.16 automata.

After minimization, we get the DFA shown in Figure 2.18, because states q ₃ , q ₄ , and q ₅ are nondistinguishable states. Hence, they get combined, and this combination becomes a dead state and, can be eliminated.

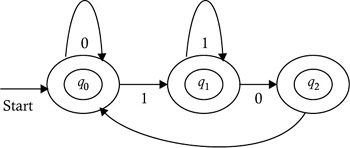
Figure 2.18: DFA after minimization.

EXAMPLE 2.8

Construct a finite automata that will accept those strings of decimal digits that are divisible by three (see Figure 2.19).

Figure 2.19: Finite automata that accepts string decimals that are divisible by three.

 

EXAMPLE 2.9

Construct a finite automata that accepts all possible strings of zeros and ones that do not contain 011 as a substring.

 

Figure 2.20 shows a transition diagram of the automata that accepts the strings containing 101 as a substring.

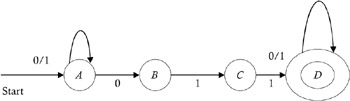
Figure 2.20: Finite automata accepts strings containing 101.

A DFA equivalent to this NFA will be:

		1
{ A }	{ A , B }	{ A }
{ A , B }	{ A , B }	{ A , C }
{ A , C }	{ A , B }	{ A , D }
{ A , D }*	{ A , B , D }	{ A , D }
{ A , B , D }*	{ A , B , D }	{ A , C , D }
{ A , C , D }*	{ A , B , D }	{ A , D }

Let us identify the states of this DFA using the names given below:

{ A }	q
{ A , B }	q 1
{ A , C }	q 2
{ A , D }	q 3
{ A , B , D }	q 4
{ A , C , D }	q 5

The transition diagram of this automata is shown in Figure 2.21.

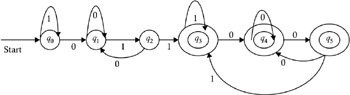
Figure 2.21: Finite automata identified by the name states A-D and q _{ˆ’ 5} .

The complement of automata shown in Figure 2.21 is illustrated in Figure 2.22.

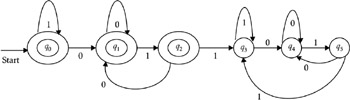
Figure 2.22: Complement to Figure 2.21 automata.

After minimization, we get the DFA shown in Figure 2.23, because the states q ₃ , q ₄ , and q ₅ are nondistinguishable states. Hence, they get combined, and this combination becomes a dead state that can be eliminated.

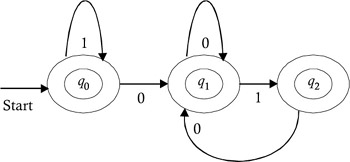
Figure 2.23: Minimization of nondistinguishable states of Figure 2.22.

EXAMPLE 2.10

Construct a finite automata that will accept those strings of a binary number that are divisible by three.

The transition diagram of this automata is shown in Figure 2.24.

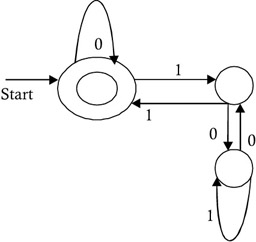
Figure 2.24: Automata that accepts binary strings that are divisible by three.